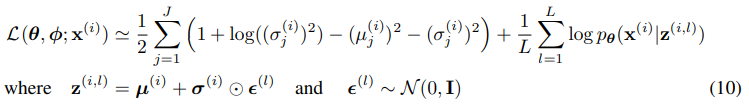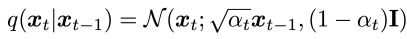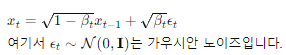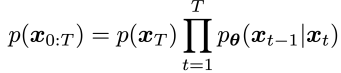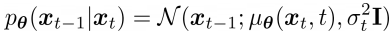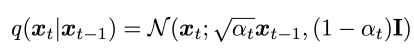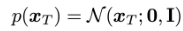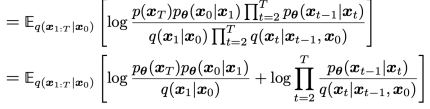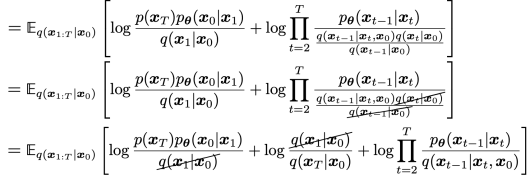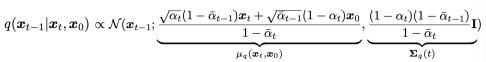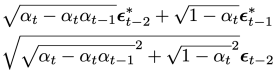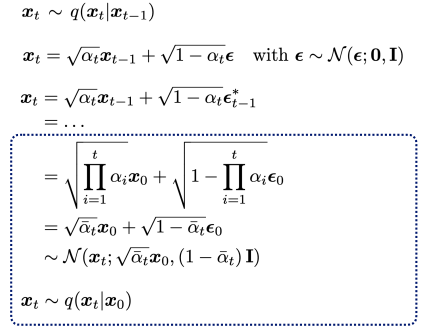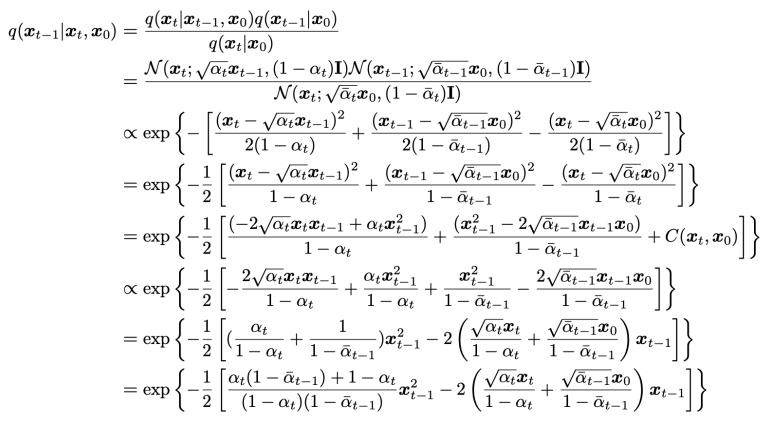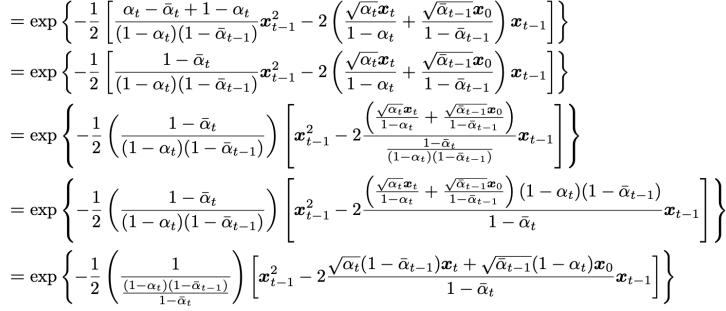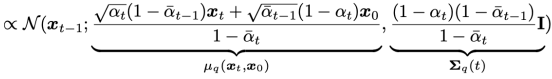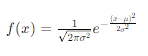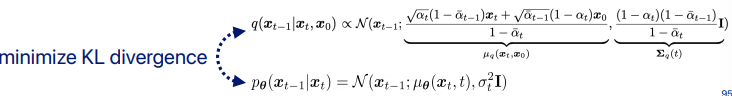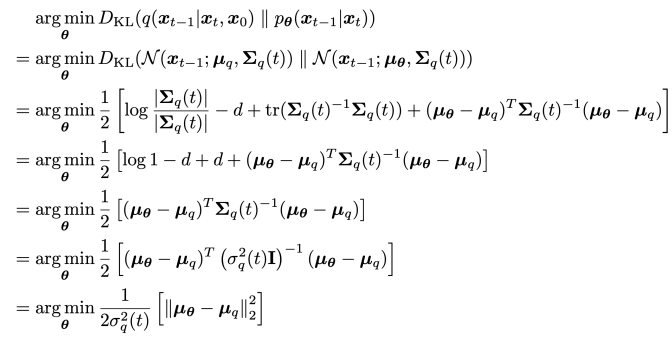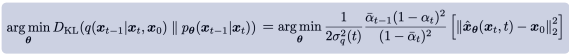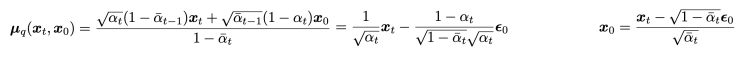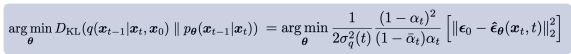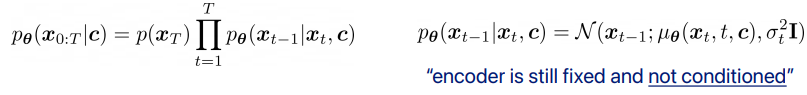Abstract
이 연구는 확산 모델이 현재 최첨단 생성 모델보다 우수한 이미지 샘플 품질을 달성할 수 있음을 보여준다. 무조건적인 이미지 합성에서는 일련의 실험을 통해 더 나은 아키텍처를 찾아냈으며, 조건부 이미지 합성에서는 classifier guidance를 사용하여 샘플 품질을 향상시켰다. 이 방법은 classifier의 기울기를 사용하여 다양성과 충실도 간의 균형을 조정하는 간단하고 효율적인 방법이다. ImageNet 데이터셋에서 FID 점수는 128×128 해상도에서 2.97, 256×256 해상도에서 4.59, 512×512 해상도에서 7.72를 기록했으며, BigGAN-deep 모델과 유사한 성능을 25회의 순방향 패스만으로 달성하면서도 분포를 더 잘 포괄했다. 마지막으로, classifier guidance는 업샘플링 확산 모델과 잘 결합되어 FID를 256×256 해상도에서 3.94, 512×512 해상도에서 3.85로 더욱 향상시켰다.
1. Introduction
지난 몇 년 동안, 생성 모델들은 인간과 유사한 자연어를 생성하고, 무한한 고품질의 합성 이미지를 만들며, 다양한 인간 음성 및 음악을 생성할 수 있는 능력을 갖추게 되었다. 이러한 모델들은 텍스트 프롬프트로부터 이미지를 생성하거나 유용한 특징 표현을 학습하는 등 다양한 방식으로 사용될 수 있다. 현재 이러한 모델들이 이미 현실적인 이미지와 소리를 생성할 수 있지만, 현 상태보다 더 나아질 여지가 많으며, 더 나은 생성 모델은 그래픽 디자인, 게임, 음악 제작 등 수많은 분야에 광범위한 영향을 미칠 수 있다.
현재 GANs는 FID, Inception Score 및 Precision과 같은 샘플 품질 지표에서 대부분의 이미지 생성 작업에서 최첨단 성능을 보여주고 있다. 그러나 일부 지표는 다양성을 충분히 포착하지 못하며, GANs는 최신 확률 기반 모델들보다 다양성을 덜 포착하는 것으로 나타났다. 또한, GANs는 훈련하기 어려우며, 신중하게 선택된 하이퍼파라미터와 정규화 기법 없이는 종종 학습이 실패한다.
GANs가 최첨단을 유지하고 있지만, 그 단점으로 인해 새로운 도메인에 확장하고 적용하기 어렵다. 이에 따라 GAN과 같은 샘플 품질을 달성하기 위해 확률 기반 모델에 대한 많은 연구가 진행되어 왔다. 이러한 모델들은 더 많은 다양성을 포착하고 GANs보다 훈련 및 확장이 용이하지만, 여전히 시각적 샘플 품질에서는 뒤처진다. 또한, VAEs를 제외하면 이러한 모델들은 샘플링 시간이 GANs보다 느리다.
확산 모델은 최근 고품질 이미지를 생성할 수 있는 것으로 입증된 확률 기반 모델의 한 종류로, distribution coverage(생성 모델이 데이터의 전체 분포를 얼마나 잘 포착하고 표현하는가 = 훈련된 데이터셋의 다양한 사례들을 잘 반영하고 있는가), stationary training objective(학습하는 동안 목표함수가 변하지 않음), 용이한 확장성 등의 바람직한 특성을 제공한다. 이 모델들은 신호에서 점진적으로 노이즈를 제거하여 샘플을 생성하며, 그 훈련 목표는 재가중된 변분 하한으로 표현될 수 있다. 이 모델들은 이미 CIFAR-10에서 최첨단 성능을 보유하고 있지만, LSUN과 ImageNet과 같은 어려운 생성 데이터셋에서는 여전히 GANs에 뒤처진다. Nichol과 Dhariwal은 이러한 모델들이 계산량이 증가할수록 성능이 안정적으로 향상되며, 업샘플링 스택을 사용하여 ImageNet 256×256 데이터셋에서도 고품질 샘플을 생성할 수 있다고 밝혔다. 그러나 이 모델의 FID는 여전히 이 데이터셋의 최첨단인 BigGAN-deep과 경쟁하기에 부족하다.
우리는 확산 모델과 GANs 간의 격차가 적어도 두 가지 요인에서 비롯된다고 가정한다: 첫째, 최근의 GAN 연구에서 사용된 모델 아키텍처가 많이 탐색되어 최적의 설계를 정제해았다는 점; 둘째, GANs는 다양성을 희생하여 충실도(생성된 샘플이 실제 데이터와 유사한 정도) 높이는 방식으로 높은 품질의 샘플을 생성할 수 있지만, 전체 분포를 커버하지는 않는다는 점이다. 우리는 이러한 이점을 확산 모델에 도입하기 위해 먼저 모델 아키텍처를 개선하고, 다양성과 충실도 간의 균형을 조정하는 방식을 고안했다. 이러한 개선을 통해 우리는 여러 지표와 데이터셋에서 새로운 최첨단 성능을 달성하였다.
이 논문의 나머지 부분은 다음과 같이 구성된다. 2장에서는 Ho et al.와 Nichol 및 Dhariwal, Song et al.의 연구에 기반한 확산 모델의 배경과 평가 설정을 설명한다. 3장에서는 FID를 크게 향상시키는 간단한 아키텍처 개선 사항을 소개한다. 4장에서는 샘플링 중 분류기의 기울기(확률을 높이거나 낮추기 위해 필요한 변화 방향)를 사용하여 확산 모델을 guide하는 방법을 설명한다. 우리는 단일 하이퍼파라미터인 분류기 기울기의 크기를 조정하여 다양성과 충실도 간의 균형을 맞출 수 있음을 발견했으며, 이 기울기 스케일 인자를 대폭 증가시켜도 적대적 예제(분류기와 같은 모델을 속이기 위해 고의적으로 조작된 입력)를 얻지 않는다. 마지막으로 5장에서는 우리의 개선된 아키텍처를 통해 unconditional 이미지 합성 작업에서 최첨단 성능을 달성하였으며, 분류기 가이던스를 사용하여 조건부 이미지 합성에서도 최첨단 성능을 달성했음을 보여준다. 분류기 가이던스를 사용할 때, 우리는 단 25번의 순방향 패스만으로도 BigGAN과 유사한 FID를 유지할 수 있음을 발견했다. 또한, 우리의 개선된 모델과 업샘플링 스택을 비교한 결과, 두 접근 방식이 상호 보완적인 개선을 제공하며, 이를 결합하면 ImageNet 256×256 및 512×512에서 최상의 결과를 얻을 수 있음을 알 수 있었다.
2. Background
이 절에서는 확산 모델에 대한 간략한 개요를 제공한다. 보다 자세한 수학적 설명은 부록 B를 참고하기 바란다.
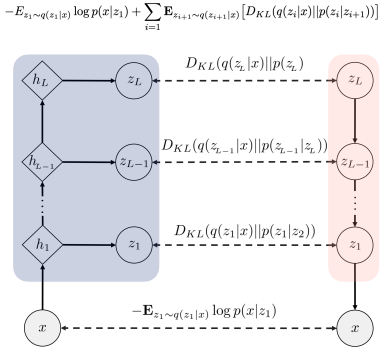
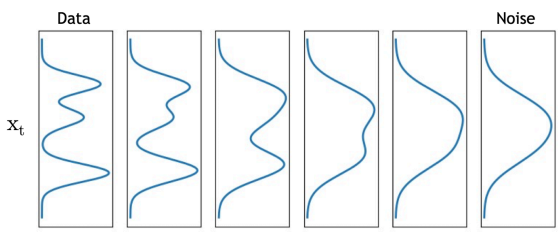
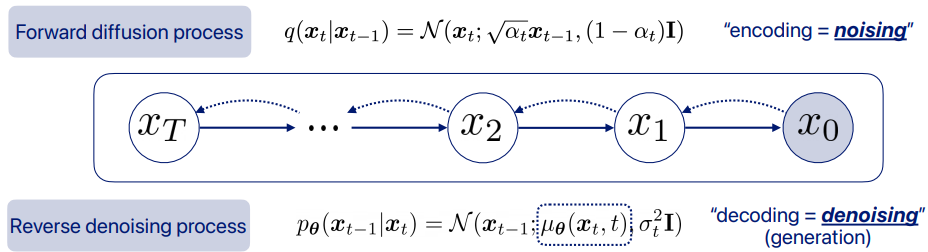
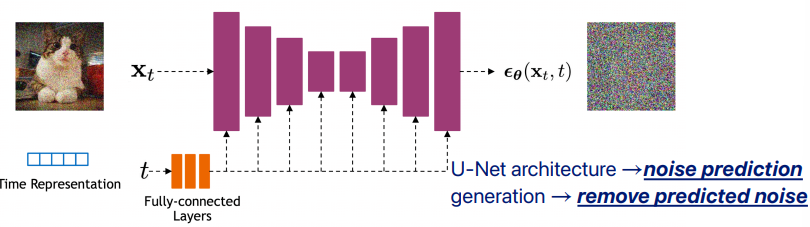
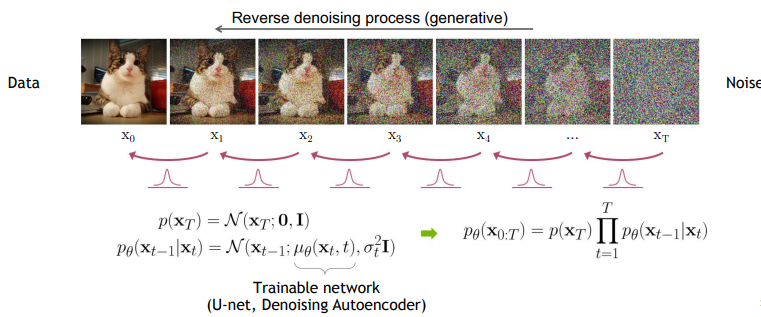
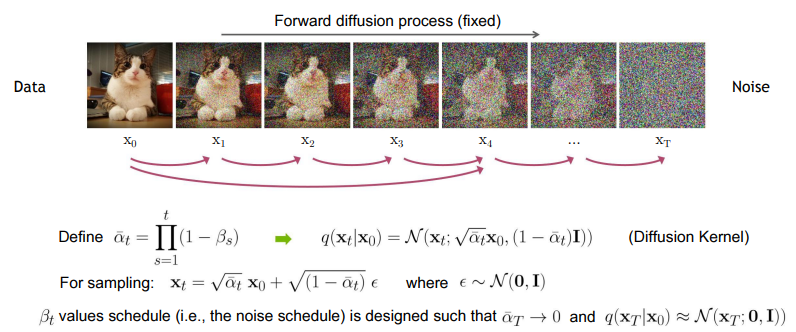
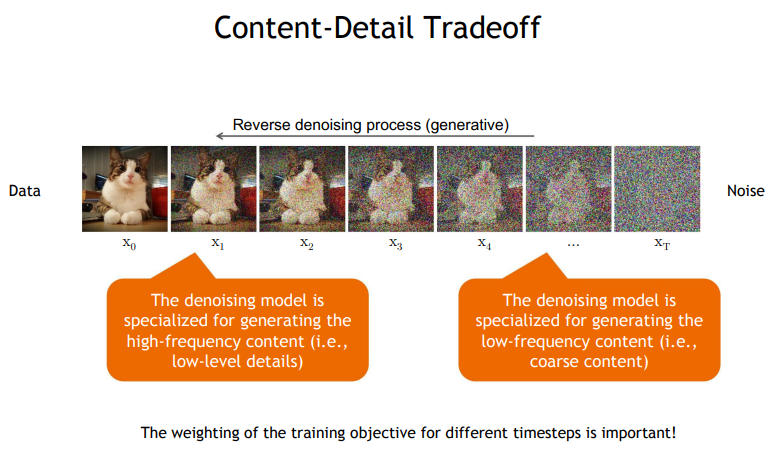
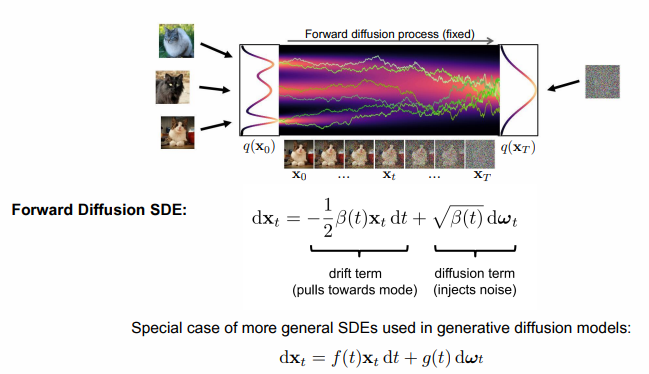
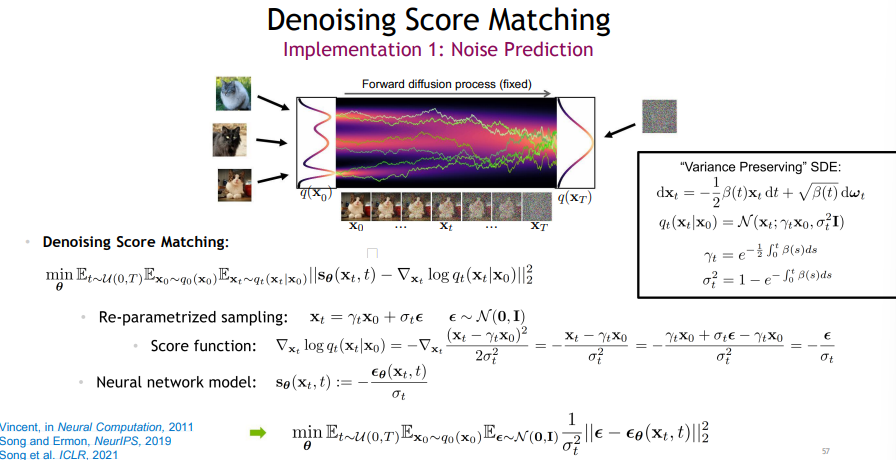
고수준에서 보면, 확산 모델은 점진적인 노이즈 추가 과정을 역으로 수행하여 분포에서 샘플을 추출한다. 구체적으로, 샘플링은 노이즈 x_T에서 시작하여 점차 노이즈가 적은 샘플 x_{T-1}, x_{T-2},...을 생성하며 최종 샘플 x_0에 도달한다. 각 시점 는 특정 노이즈 수준에 대응하며, x_t는 시점 t에 따라 신호 x_0와 일부 노이즈 ϵ의 혼합으로 생각할 수 있다. 이 논문에서는 노이즈 ϵ이 자연 이미지에 잘 작동하고 다양한 유도 과정을 단순화하는 대각 가우시안 분포에서 나오는 것으로 가정한다.
확산 모델은 x_t에서 x_{t-1}로 약간 더 "노이즈가 제거된" 샘플을 생성하도록 학습된다. Ho et al. [25]는 이 모델을 함수 ϵ_θ(x_t,t)로 매개변수화하여, 노이즈가 섞인 샘플 x_t의 노이즈 성분을 예측한다고 설명한다. 이 모델을 훈련시키기 위해, 미니배치의 각 샘플은 데이터 샘플 x_0, 시점 t및 노이즈 ϵ을 무작위로 선택하여 생성된 노이즈가 추가된 샘플 x_t (식 17)를 사용한다. 훈련 목표는 단순한 평균 제곱 오차 손실로, 실제 노이즈와 예측된 노이즈 간의 차이 ∣∣ϵ_θ(x_t,t)−ϵ∣∣^2를 최소화하는 것이다 (식 26).
노이즈 예측기 ϵ_θ(x_t,t)로부터 샘플을 생성하는 방법은 즉각적으로 명확하지 않다. 확산 샘플링은 x_T에서 시작하여 x_t에서 x_{t-1}을 반복적으로 예측하는 방식으로 진행된다. Ho et al. [25]는 합리적인 가정 하에서 x_t가 주어졌을 때 x_{t-1}의 분포 p_θ(x_{t−1}∣x_t)를 대각 가우시안 N(x_{t−1};μ_θ(x_t,t),Σ_θ(x_t,t))로 모델링할 수 있으며, 이때 평균 μ_θ(x_t,t)는 ϵ_θ(x_t, t)의 함수로 계산될 수 있음을 보여준다 (식 27). 이 가우시안 분포의 분산 Σ_θ(x_t,t)는 고정된 상수로 설정하거나 별도의 신경망 헤드로 학습할 수 있으며, 두 접근법 모두 총 확산 단계 수 T가 충분히 클 때 고품질 샘플을 생성할 수 있다.
Ho et al. [25]는 실제 변분 하한 L_vlb보다 단순한 평균 제곱 오차 목표 L_simple가 실무적으로 더 잘 작동한다고 언급한다. 또한, 이 목표로 훈련하고 해당 샘플링 절차를 사용하는 것이 Song과 Ermon [58]의 논문에서 다중 노이즈 수준으로 훈련된 모델에서 샘플링하는 데 사용하는 Langevin dynamics 기반의 비슷한 절차와 동등하다고 언급한다. 우리는 종종 "확산 모델"이라는 용어를 이러한 모델들의 양쪽 클래스를 지칭하는 약어로 사용한다.
2.1 Improvements
최근 연구들로 diffusion model이 개선되었는데 다음과 같다.
1. reverse process variance의 매개변수화
Ho et al. [25]에서는 역 과정(reverse process)에서 사용하는 분산 Σ_θ(x_t,t)을 고정된 상수로 설정했다. 그러나 Nichol과 Dhariwal [43]은 이를 신경망의 출력으로 매개변수화하여 더 나은 샘플링 성능을 얻을 수 있음을 발견했다. 이들은 분산 Σ_θ(x_t,t)을 다음과 같이 정의한다:

여기서 β_t와 β~_t는 Ho et al. [25]에서 정의된 상한과 하한 분산 값을 나타낸다. v는 신경망의 출력으로, 이 두 값 사이를 보간한다. 이 방법은 샘플링 단계가 적을 때에도 샘플 품질을 유지하면서 성능을 향상시다.
2. 하이브리드 목표
Nichol과 Dhariwal [43]은 ϵ_θ(x_t, t)와 Σ_θ(x_t,t)를 훈련하기 위한 혼합 손실 함수를 제안했다. 이들은 단순 손실 L_simple과 변분 하한 L_vlb를 가중합하여 사용한다. 이를 통해 reverse process에서의 분산을 학습하게 되며, 샘플링 단계 수를 줄여도 샘플 품질의 큰 저하 없이 샘플링이 가능하다. 연구에서는 이 목표함수와 매개변수화를 채택하였다.

3. DDIM
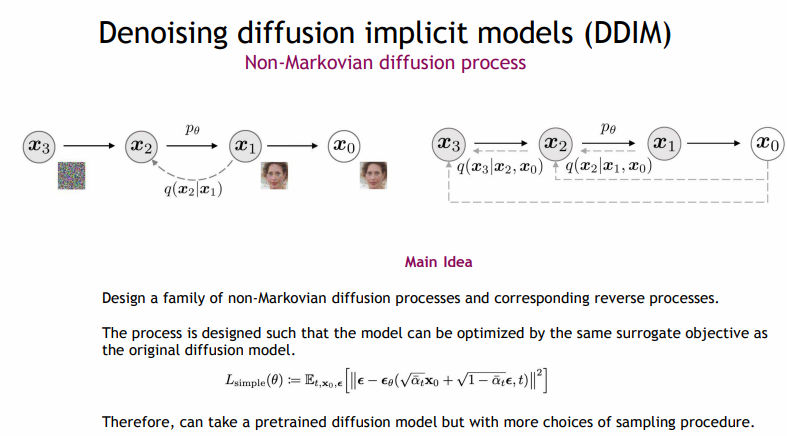
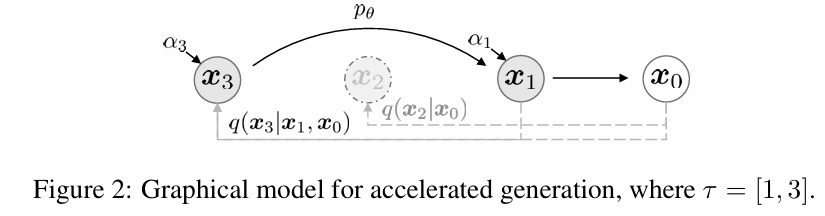
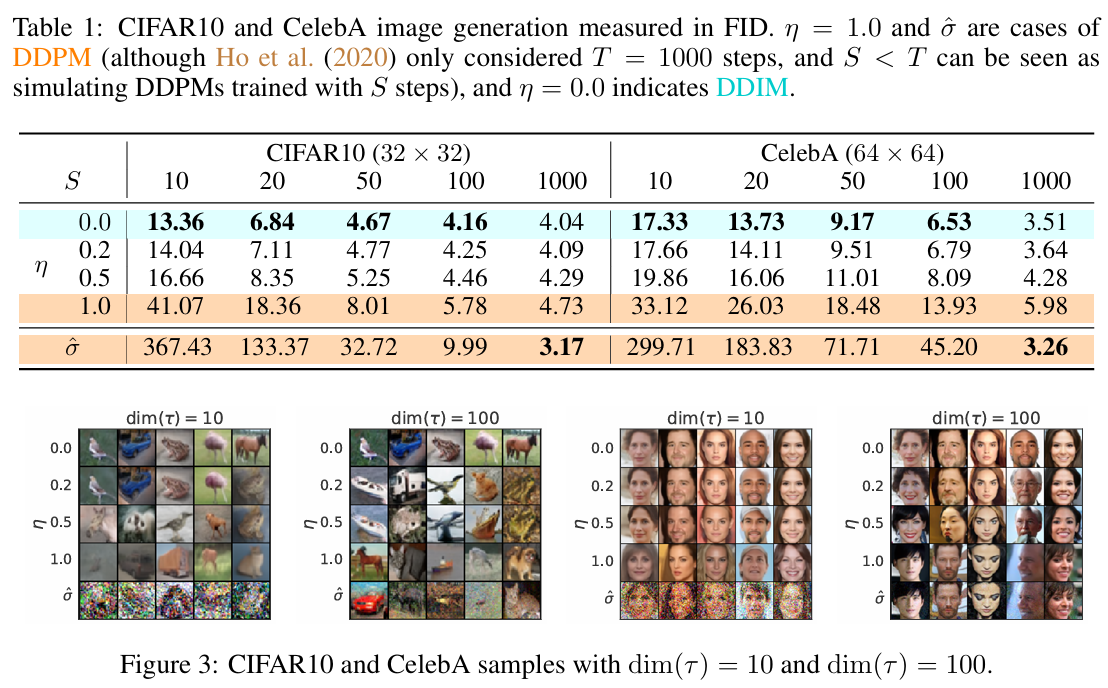
Song et al.은 DDPM의 대안으로 DDIM을 제안했다. DDIM은 동일한 forward marginals를 가지면서 비마르코브 노이즈 추가 과정을 사용한다. 이 과정은 역 노이즈의 분산을 조정하여 다양한 역 샘플러를 생성할 수 있다. 특히 노이즈를 0으로 설정하면 임의의 모델 ϵ_θ(x_t, t)를 결정론적인 mapping으로 전환할 수 있어 샘플링 단계를 줄이면서도 고품질의 이미지를 생성할 수 있다. Nichol과 Dhariwal [43]은 50단계 이하의 샘플링 시 이 방법이 유리하다고 밝혔으며, 본 연구에서도 이 접근 방식을 사용함.
2.2 Sample Quality Metrics
모델 간의 샘플 품질 비교를 위해 다음과 같은 지표를 사용하여 정량적 평가를 수행한다. 이러한 지표는 실무에서 자주 사용되며 인간의 판단과 잘 일치하지만, 샘플 품질 평가의 완벽한 대체물은 아니며, 더 나은 평가 지표를 찾는 것은 여전히 해결되지 않은 문제이다.
Inception Score (IS)는 Salimans et al. [54]에 의해 제안되었으며, 모델이 전체 ImageNet 클래스 분포를 얼마나 잘 포착하는지와 동시에 개별 샘플이 단일 클래스의 설득력 있는 예제를 생성하는지를 측정한다. 이 지표의 단점은 전체 분포를 포괄하거나 클래스 내 다양성을 포착하는 것을 보상하지 않으며, 데이터셋의 일부 하위 집합만 기억하는 모델도 높은 IS를 가질 수 있다는 점이다 [3]. IS보다 더 나은 다양성 포착을 위해 Fréchet Inception Distance (FID)는 Heusel et al. [23]에 의해 제안되었으며, 이는 Inception Score보다 인간의 판단과 더 일치한다고 주장했다. FID는 Inception-V3 [62] 잠재 공간에서 두 이미지 분포 간의 거리를 대칭적으로 측정한다. 최근에, sFID는 Nash et al. [42]에 의해 제안되었으며, 표준 합성 특징 대신 공간적 특징을 사용하는 FID의 버전이다. 이들은 이 지표가 공간적 관계를 더 잘 포착하며, 일관된 고수준 구조를 가진 이미지 분포에 보상을 준다고 밝혔다. 마지막으로, Kynkäänniemi et al. [32]는 향상된 Precision과 Recall 지표를 제안하여, 샘플 충실도를 모델 샘플이 데이터 매니폴드에 속하는 비율(Precision)과 다양성을 데이터 샘플이 샘플 매니폴드에 속하는 비율(Recall)로 각각 측정한다.
우리는 FID를 기본 지표로 사용하여 전체 샘플 품질을 비교한다. 이는 다양성과 충실도를 모두 포착하며, 최첨단 생성 모델 연구에서 사실상 표준 지표로 사용되어 왔다 [27, 28, 5, 25]. 우리는 충실도를 측정하기 위해 Precision 또는 IS를 사용하고, 다양성 또는 분포 커버리지를 측정하기 위해 Recall을 사용한다. 다른 방법과 비교할 때는 가능한 경우 공개 샘플이나 모델을 사용하여 이 지표들을 다시 계산한다. 이는 두 가지 이유 때문이다: 첫째, 일부 논문 [27, 28, 25]은 쉽게 접근할 수 없는 훈련 세트의 임의 하위 집합과 비교하고, 둘째, 미세한 구현 차이가 FID 값에 영향을 줄 수 있기 때문이다 [45]. 일관된 비교를 위해, 우리는 reference batch로 전체 훈련 세트를 사용하고 [23, 5], 모든 모델에 대해 동일한 코드베이스를 사용하여 지표를 평가한다.
3. Architecture Improvements
이 섹션에서는 확산 모델의 샘플 품질을 개선하기 위해 여러 아키텍처 변형을 실험적으로 조사하였다.
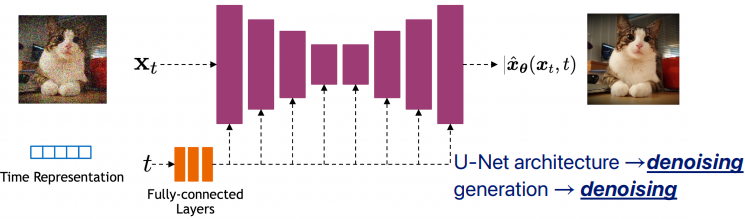
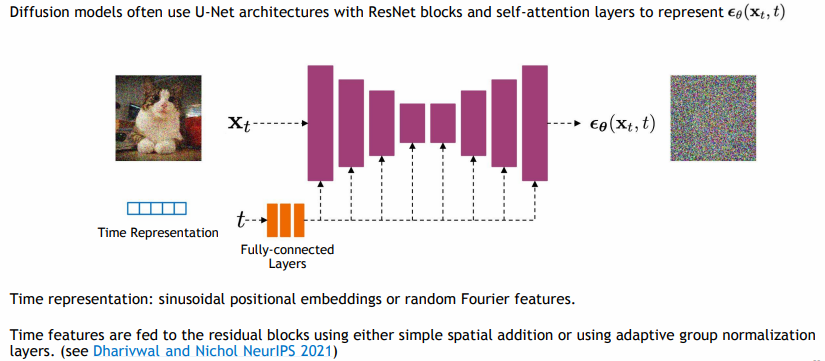
Ho et al. [25]는 확산 모델을 위한 U-Net 아키텍처를 도입하였으며, Jolicoeur-Martineau et al. [26]은 이전의 아키텍처 [58, 33]에 비해 샘플 품질이 상당히 향상된 것을 발견하였다. U-Net 모델은 residual layers와 다운샘플링 합성곱 스택을 사용하고, 이어서 residual layers와 업샘플링 합성곱로 동일한 공간 크기를 가진 레이어를 연결하는 스킵 연결을 포함한다. 또한, 이들은 16×16 해상도에서 단일 헤드를 사용하는 글로벌 어텐션 레이어를 사용하고, 각 residual 블록에 타임스텝 임베딩을 투영하였다. Song et al. [60]은 U-Net 아키텍처의 추가적인 변경이 CIFAR-10 [31]과 CelebA-64 [34] 데이터셋에서 성능을 향상시켰음을 발견하였다. 우리는 ImageNet 128×128에서 동일한 결과를 보이며, 더 큰 해상도의 더 크고 다양한 데이터셋에서도 아키텍처가 샘플 품질에 큰 영향을 미칠 수 있음을 확인하였다.
다음과 같은 아키텍처 변경 사항을 탐구하였다
- 깊이 증가 vs. 너비 증가: 모델 크기는 일정하게 유지하며 깊이와 너비를 조절함.
- 어텐션 헤드 수 증가.
- 16×16 해상도뿐만 아니라 32×32, 16×16, 8×8 해상도에서도 어텐션 사용.
- BigGAN의 잔여 블록을 사용하여 업샘플링 및 다운샘플링 수행.
- 잔여 연결을 √1/2로 스케일링.
이 섹션의 모든 비교에서, 우리는 ImageNet 128×128 데이터셋에 대해 배치 크기 256으로 모델을 훈련하고, 250 샘플링 단계를 사용하여 샘플링을 수행하였다. 우리는 위의 아키텍처 변경 사항을 적용하여 모델을 훈련시키고, 훈련 중 두 개의 다른 지점에서 FID를 평가하여 성능을 비교하였다(Table 1).

Residual connections 재스케일링을 제외한 모든 다른 수정 사항이 성능을 향상시키며 긍정적인 복합 효과를 나타냈다. Figure 2에서 볼 수 있듯이, 깊이를 증가시키는 것이 성능에 도움이 되지만, 훈련 시간이 증가하여 동일한 성능에 도달하는 데 더 오랜 시간이 걸리므로 후속 실험에서는 이 변경을 사용하지 않기로 결정하였다.

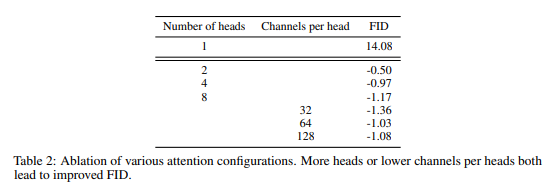
우리는 또한 Transformer 아키텍처 [66]에 더 잘 맞는 다른 어텐션 구성을 연구하였다. 이를 위해, 어텐션 헤드를 고정하거나 각 헤드당 채널 수를 고정하는 실험을 수행하였다. 나머지 아키텍처로는 128 기본 채널, 해상도당 2개의 잔여 블록, 다중 해상도 어텐션, BigGAN 업/다운샘플링을 사용하였으며, 모델을 700K 반복 동안 훈련시켰다. Table 2는 우리의 결과를 보여주며, 더 많은 헤드나 헤드당 적은 채널 수가 FID를 개선함을 나타낸다. Figure 2에서 볼 수 있듯이, wall-clock time 측면에서 64 채널이 최적이므로, 우리는 기본값으로 64 채널을 사용하기로 결정하였다.
3.1 Adaptive Group Normalization
이 절에서는 적응형 그룹 정규화(AdaGN) 레이어에 대해 실험한다. 이 레이어는 그룹 정규화 작업 후 각 잔여 블록에 타임스텝과 클래스 임베딩을 포함하며, 이는 adaptive instance norm [27] 및 FiLM [48]과 유사하다. 우리는 이 레이어를 다음과 같이 정의한다: AdaGN(h, y) = y_s * GroupNorm(h) + y_b, 여기서 h는 첫 번째 합성곱 이후 잔여 블록의 중간 활성화이고, y = [y_s, y_b]는 타임스텝과 클래스 임베딩의 linear projection으로부터 얻어진다.
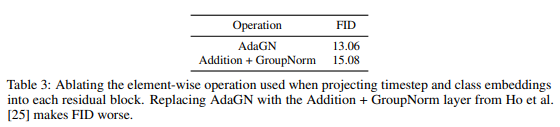
초기 확산 모델에서 AdaGN이 성능을 향상시키는 것을 확인하였고, 따라서 모든 실험에서 기본적으로 포함되었다. Table 3에서 이 선택을 제거하여 실험한 결과, 적응형 그룹 정규화 레이어가 FID를 향상시키는 것으로 나타났다. 두 모델 모두 기본 채널 128개, 해상도당 2개의 잔여 블록, 헤드당 64채널을 갖는 다중 해상도 어텐션, 그리고 BigGAN 업/다운샘플링을 사용하였으며, 700K 반복 동안 훈련되었다.
이 논문의 나머지 부분에서는 다음과 같은 최종 개선된 모델 아키텍처를 기본 설정으로 사용한다:
- Resolution당 2개의 residual block
- 가변 너비
- Head당 64개 채널이 있는 multiple head
- 32, 16, 8 resoltion에서의 attention
- BIGAN의 residual block으로 up/downsampling
- Residual block에 timestep embedding과 class embedding을 주입하기 위한 AdaGN
4. Classifier Guidance
잘 설계된 아키텍처를 사용하는 것 외에도, 조건부 이미지 합성을 위한 GANs [39, 5]는 클래스 레이블을 많이 활용한다. 이는 종종 클래스-조건부 정규화 통계 [16, 11]와 분류기처럼 작동하도록 설계된 헤드를 가진 판별기 [40]의 형태로 나타난다. 이러한 모델의 성공에 클래스 정보가 중요한 또 다른 증거로, Lucic et al. [36]은 레이블이 제한된 상황에서 합성 레이블을 생성하는 것이 도움이 된다는 것을 발견했다.
GANs에 대한 이러한 관찰을 바탕으로, 우리는 확산 모델을 클래스 레이블에 조건화하는 다양한 방법을 탐구하는 것이 합리적이다. 우리는 이미 AdaGN에 클래스 정보를 통합하고 있다(3.1절). 여기에서는 다른 접근 방식을 탐구한다: 분류기 p(y|x)를 활용하여 diffusion generator를 개선하는 방법이다. Sohl-Dickstein et al. [56]과 Song et al. [60]은 사전 훈련된 확산 모델을 분류기의 기울기를 사용하여 조건화할 수 있는 한 가지 방법을 제시한다. 구체적으로, 우리는 노이즈가 포함된 이미지 x_t에 대해 분류기 p_ϕ(y∣x_t,t)를 훈련하고, 그런 다음 기울기 ∇_{x_t}logp_ϕ(y∣x_t,t)를 사용하여 확산 샘플링 과정을 임의의 클래스 레이블 y로 안내할 수 있다.
이 절에서는 먼저 분류기를 사용하여 조건부 샘플링 프로세스를 도출하는 두 가지 방법을 검토한다. 그런 다음, 이러한 분류기를 실제로 사용하여 샘플 품질을 개선하는 방법을 설명한다. 우리는 간결함을 위해 p_ϕ(y∣x_t,t)=p_ϕ(y∣x_t)와 ϵ_θ(x_t,t)=ϵθ(x_t)를 표기하지만, 이는 각 타임스텝 에 대해 별도의 함수를 나타내며, 훈련 시 모델은 입력 t에 대해 조건화되어야 함을 유의해야 한다.
4.1 Conditional Reverse Noising Process
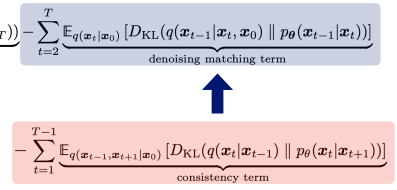
Unconditional reverse noising process가 pθ(xt|xt+1)인 diffusion model을 레이블 로 컨디셔닝하면 다음과 같이 샘플링하는 것으로 충분하다.
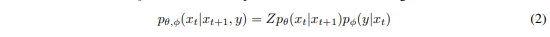
여기서 Z는 정규화 상수이다(증명은 부록 H에 있다). 이 분포에서 정확하게 샘플링하는 것은 일반적으로 실행 불가능하지만, Sohl-Dickstein et al. [56]은 이를 약간 왜곡된 가우시안 분포로 근사할 수 있음을 보여준다. 여기서는 이 유도를 검토한다.
우리의 확산 모델은 가우시안 분포를 사용하여 타임스텝 xt_1에서 이전 타임스텝 x_t를 예측한다:

우리는 logp_ϕ(y∣x_t)의 곡률이 Σ−1에 비해 낮다고 가정할 수 있다. 이 가정은 무한한 확산 단계에서 ∥Σ∥→0일 때 합리적이다. 이 경우, logp_ϕ(y∣x_t)를 x_t=μ 주변에서 테일러 전개를 사용하여 다음과 같이 근사할 수 있다:
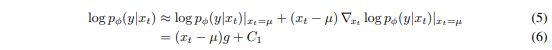
여기서 이고 은 상수이다. 이를 대입하면 다음과 같다.
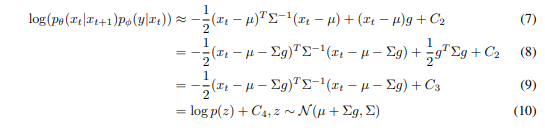
는 정규화 상수 Z에 해당하기 때문에 무시할 수 있다. 따라서 conditional transition operator를 unconditional transition operator와 유사한 가우시안 분포로 근사할 수 있으며, 이 때 평균이 만큼 이동한다. Algorithm 1은 해당 샘플링 알고리즘을 요약한다. 뒤의 섹션에서 기울기에 대한 scale factor 를 포함하며 자세히 설명한다.

4.2 Conditional Sampling for DDIM
위의 조건부 샘플링 유도는 확률적 확산 샘플링 과정에만 유효하며, DDIM [57]과 같은 결정적 샘플링 방법에는 적용할 수 없다. 이를 위해, 우리는 Song et al. [60]에서 제안한 점수 기반 조건화 기법을 사용한다. 이 기법은 확산 모델과 점수 매칭 [59] 간의 관계를 활용한다. 특히, 샘플에 추가된 노이즈를 예측하는 모델 ϵ_θ(x_t)가 주어지면, 다음과 같이 점수 함수를 유도할 수 있다:
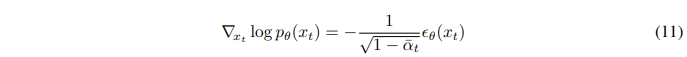
이를 p(x_t)p(y∣x_t)의 점수 함수에 대입하면 다음과 같다:
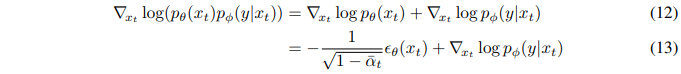
마지막으로, 결합 분포의 점수에 해당하는 새로운 epsilon 예측 ϵ^(x_t)을 다음과 같이 정의할 수 있다:
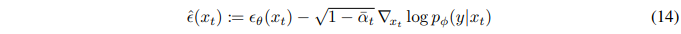
이후, 수정된 노이즈 예측 ϵ^(x_t)을 사용하여 일반 DDIM에서 사용하는 것과 동일한 샘플링 절차를 사용할 수 있다. 알고리즘 2는 해당 샘플링 알고리즘을 요약한다.

4.3 Scaling Classifier Gradients
분류기 가이던스를 대규모 생성 작업에 적용하기 위해, 우리는 ImageNet에서 분류 모델을 훈련시켰다. 분류기 아키텍처는 UNet 모델의 다운샘플링 부분에 8x8 레이어에서 최종 출력을 생성하기 위한 어텐션 풀링을 추가한 것이다. 이러한 분류기는 대응하는 확산 모델과 동일한 노이즈 분포에서 훈련되며, 오버피팅을 줄이기 위해 랜덤 크롭을 추가한다. 훈련이 완료된 후, 우리는 알고리즘 1에 따라 식 (10)을 사용하여 분류기를 확산 모델의 샘플링 과정에 통합하였다.
초기 실험에서는 무조건적 ImageNet 모델에서 분류기 기울기를 1보다 큰 상수로 스케일링하는 것이 필요함을 발견하였다. 스케일 1을 사용할 때, 최종 샘플에 대해 분류기가 합리적인 확률(약 50%)을 할당하였으나, 시각적으로 샘플이 의도된 클래스와 일치하지 않았다. 분류기 기울기를 증가시키면 이 문제가 해결되었으며, 분류기의 클래스 확률이 거의 100%로 증가하였다. Figure 3은 이 효과의 예를 보여준다.

분류기 기울기 스케일링의 효과를 이해하기 위해, s⋅∇_xlogp(y∣x)=∇_xlog1/Zp(y∣x)^s를 고려하자. 여기서 는 임의의 상수이다. 결과적으로, 조건화 과정은 p(y∣x)^s에 비례하는 재정규화된 분류기 분포에 이론적으로 기반을 두고 있다. s>1일 때, 이 분포는 p(y∣x)보다 더 날카로워지며, 이는 더 높은 충실도(하지만 덜 다양한) 샘플을 생성하는 데 유리할 수 있다.
위의 유도에서는 기본 확산 모델이 무조건적인 모델 p(x)이라고 가정했다. 조건부 확산 모델 p(x∣y)을 훈련시키고 동일한 방식으로 분류기 가이던스를 사용할 수도 있다. Table 4는 분류기 가이던스가 무조건적 모델과 조건부 모델 모두의 샘플 품질을 크게 향상시킬 수 있음을 보여준다.
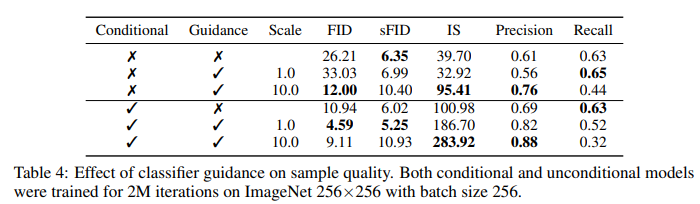
충분히 높은 스케일을 사용하면, 가이던스를 받은 unconditional 모델이 가이던스를 받지 않은 조건부 모델의 FID에 가까워질 수 있지만, 클래스 레이블을 직접 사용하여 훈련하는 것이 여전히 도움이 된다. 조건부 모델에 가이던스를 추가하면 FID가 더욱 개선된다.
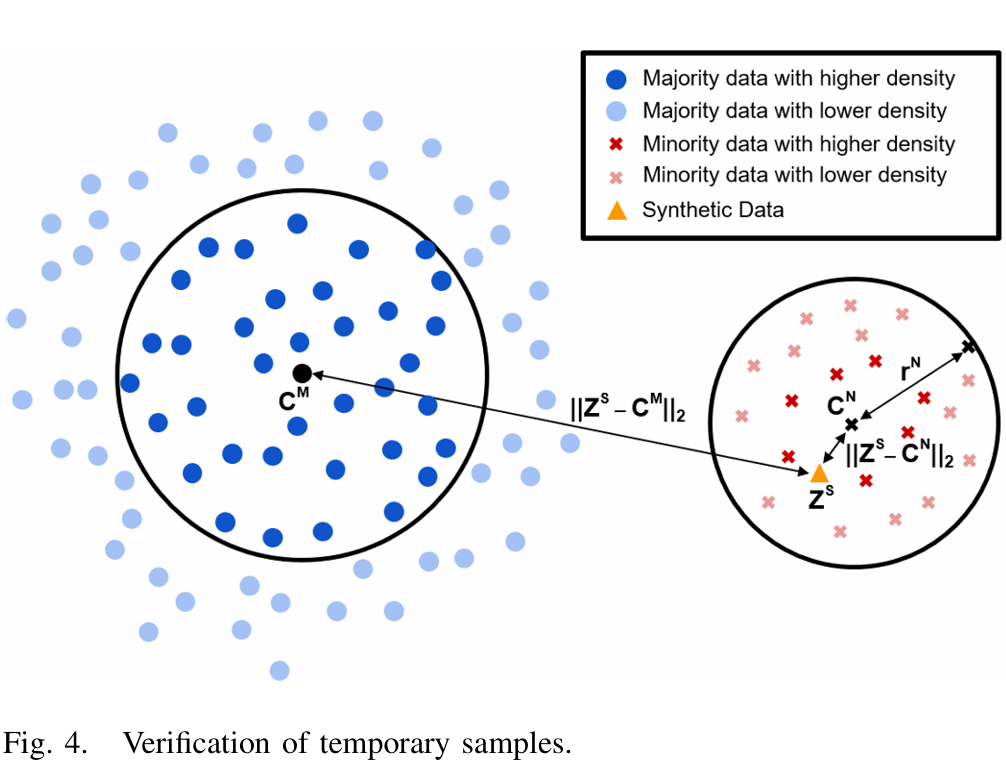
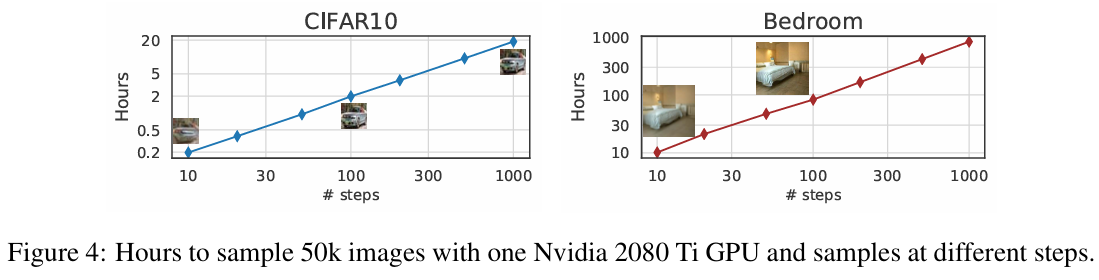
Table 4는 또한 분류기 가이던스가 정밀도를 향상시키는 반면, 리콜은 감소시키는 효과가 있음을 보여준다. 이는 샘플의 충실도와 다양성 간의 절충을 야기한다. Figure 4에서는 기울기 스케일에 따라 이러한 절충이 어떻게 변하는지 명확하게 평가하였다.
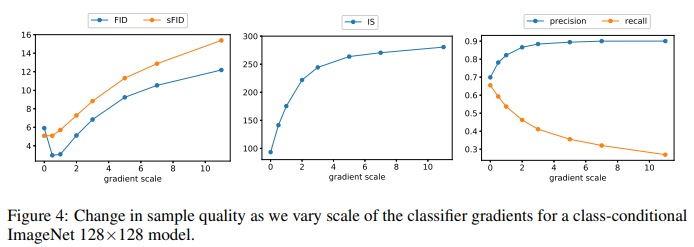
기울기 스케일을 1.0 이상으로 조정하면, 리콜(다양성의 측정치)은 점차 감소하고, 정밀도와 IS(충실도의 측정치)는 증가하는 경향을 보인다. FID와 sFID는 다양성과 충실도 모두에 의존하므로, 최적의 값은 중간 지점에서 얻어진다.
또한, Figure 5에서는 BigGAN의 트렁케이션 기법과 우리의 가이던스를 비교하였다.
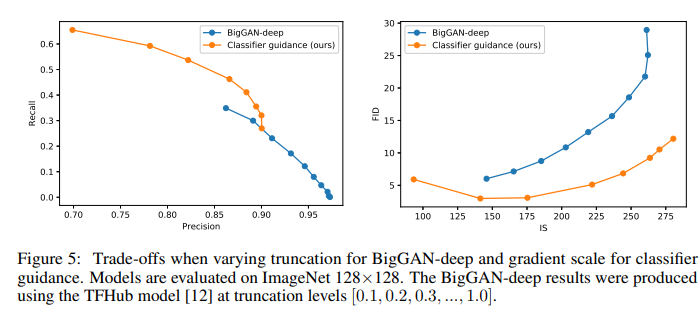
그 결과, FID와 Inception Score 사이의 절충에서 분류기 가이던스가 BigGAN-deep보다 일관되게 더 나은 성능을 보임을 확인하였다. 그러나 정밀도/리콜 절충에 있어서는, 분류기 가이던스가 특정 정밀도 임계값까지는 더 나은 선택이지만, 그 이후로는 더 나은 정밀도를 달성할 수 없다는 점이 명확하지 않다.
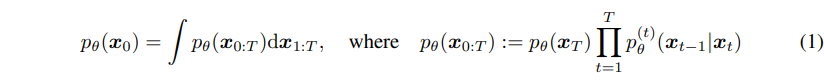

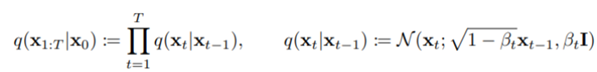

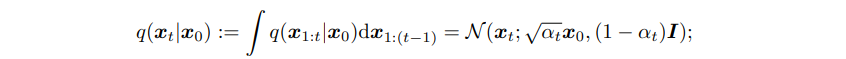
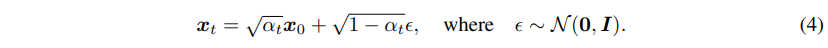
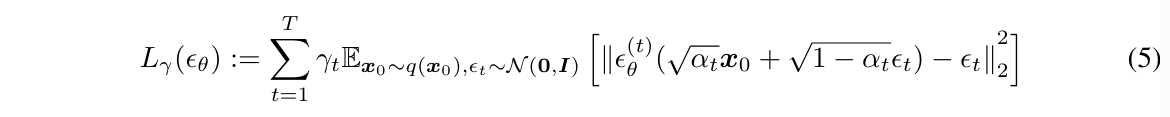
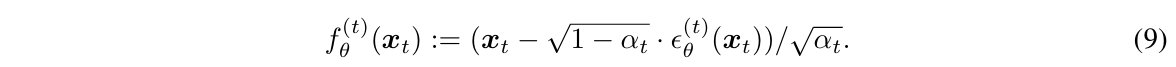
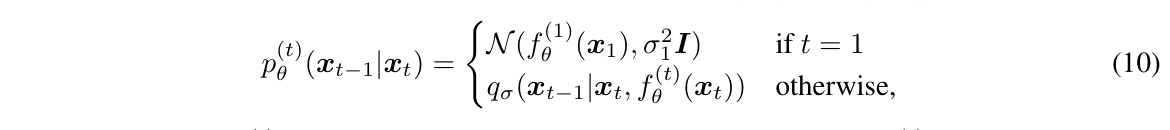
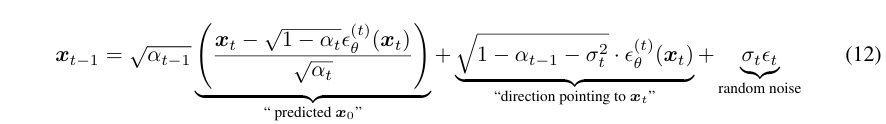
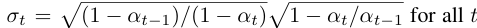
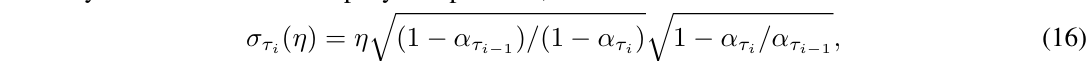


































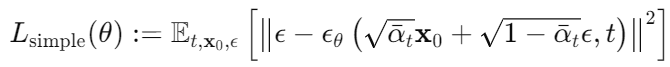
















































 이어서
이어서