Preview 영상이 이해가 하나도 안가서 이번학기에 들은 수업자료를 먼저 되짚어보겠다.
1. MLDL2 수업 - VAE

0. Intro.
Data distribution을 알면 p(x)를 기반으로 새로운 samples를 만들거나 새로운 데이터 $\widetilde{x}$가 기존에 관측된 data와 유사한지 판단할 수 있다. 따라서 우리는 model을 통해 data distribution을 approximate하는 것이 목표이고 data distribution을 approximate한다는 것은 observed data x에 대해 likelihood p(x)를 maximize하는 것과 같다.(model에서도 관찰된 데이터가 '관찰'될 확률을 높인다는 것)

하지만 우리의 data는 보통 high-dimensional하기 때문에 그 분포는 매우 complex하다. 이를 해결하기 위해 indirect approach인 laten variable methods를 사용한다.
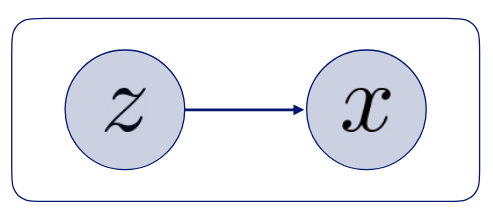
이 접근방법은 우리의 관측된 x가 관측되지 않는 미지의 변수인 z로부터 생성됬다고 가정하는 것이다. 보통 이 미지의 변수를 latent variable 혹은 hidden variable인데 low-dimensional임이 자연스럽다.(high-dimensional하면 도입할 이유가 없다!)
이제 우리는 modeling하려던 p(x) 대신 p(x,z)를 예측하면 되고 이 p(x,z)는 p(z)와 p(x|z) 두개의 곱으로 이루어진다. 즉,
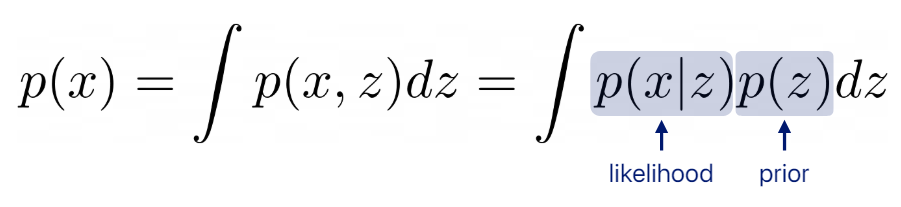
여기서의 likilihood는 우리가 도입한 변수인 z와 x 사이간의 likelihood이고 p(z)는 우리가 가정한, 추측한 확률이므로 prior probability로 해석한다.
이렇게 latent variable을 도입한 예시로 gaussian을 활용한 방법이 있다.
Data distribution이 gaussians의 mixtue N개로 되어있다고 가정하여 data가 그 중 하나로부터 생성되었다고 해석한다.
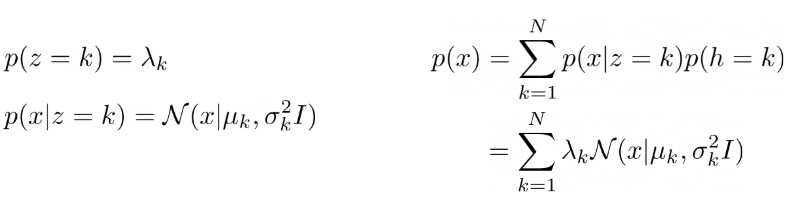
이 관점의 특징은 z를 discrete variabe로 본다는 것이다. 따라서 z의 분포는 각 값을 가질 확률로 표현되는 discrete distribution이고 각 data는 자신이 generate된 gaussian의 index인 component index를 갖는다.
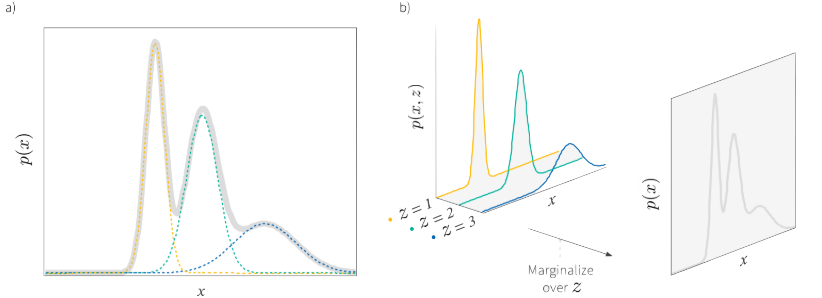
이 아이디어를 확장한 latent variable model로 non-linear lattent variable model이 있는데 이 모델은 latent variable z가 countinuous variable이고 nomarl prior로 부터 sampling되었다고 가정한다. 즉,

그런데 Conditional probability의 mean을 예측하는 f(z)는 신경망 같은 함수인 non-linear function 이기 때문에 위 적분이 불가능하다.(선형이면 가능) 그러니까 지금 생긴 문제를 정리해보면 우리는 p(x)의 likelihood를 maximize해야 하는데 직접 접근하는 것이 어려워 latent variable을 도입했지만 그럼에도 불구하고 closed form이 존재하지 않는 상황인 것이다.
따라서 이를 해결하기 이해 lower bound를 도입해 proxy objectibve(대리 목적함수)를 사용한다.
1 . ELBO: Evidence Lower Bound
ELBO에서 evidence는 observed data의 log-likelihood를 의미한다. 즉, ELBO는 위에서 말한 proxu objective인것.
이제 ELBO를 어떻게 해석할지 알아보기 위해 Jensen's Inequality로 식을 전개해볼 것인데 먼저 Jensen's Inequality는 다음과 같다.
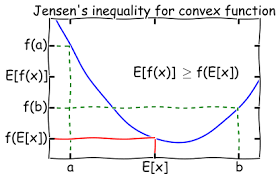
log function은 concave하기 때문에 평균의 함수값이 함수값의 평균보다 큰 성질을 이용할 것이다. 그럼,

이렇게 식이 전개되고
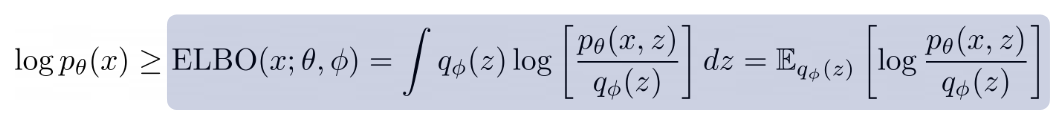
ELBO는 위와 같이 쓸 수 있다. 여기서 세타는 p를 결정하는 parameters이고 파이는 q를 결정하는 파라미터이다.
2. Variational Inference(VI)
그 다음은 ELBO를 최대화 하는 과정을 배울 것인데 처음 배울 때 매우 신기한 아이디어인 VI에 대해 알아보자. ELBO를 이렇게 전개할 수도 있다.

x와 z의 joint distribution에 z에 대한 posterior를 도입한 것인데(이게 참 웃긴게 우리는 z가 x를 만들었다고 가정했지만 여기서의 확률은 given x, z의 분포에서 얻은 확률이다.) ELBO가 원래 우리가 구하려던 evidence에 z의 분포와 p(z|x)의 KL-divergene를 뺀 것이라는 것이다. 즉, tight한 바운드는 두 분포 z를 예측한 분포(q), z의 posterior이 같았을 때이다.
그럼 우리는 ELBO를 어떻게 maximize할까? 우리는 E-M Method(Expectation-Maximization Method, velog에 올라와있는데 추후 가져올 예정..)를 통해 세타와 파이를 번갈아가면서 최적화 해 evidence의 max에 가까워질 수 있다. 즉, 간접적으로 intractable(적분 불가능한) evidence를 optimize하는 것이다.
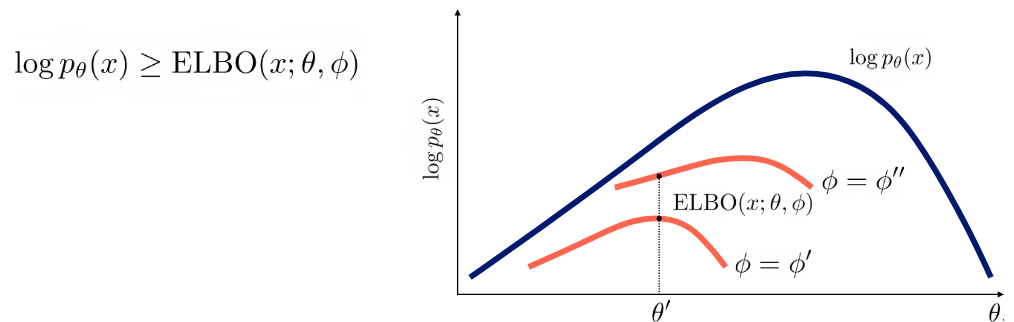
위에서 말한 expectation과 maximization 과정은 각각 tight한 bound를 만드는(파이를 update), bound를 개선하는(세타를 update)하는 것인데 그림으로 나타내면 다음과 같다.
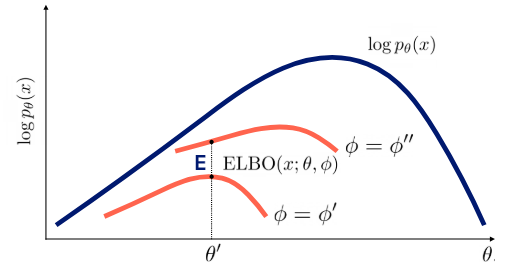
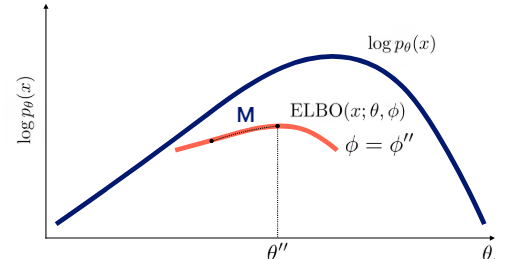
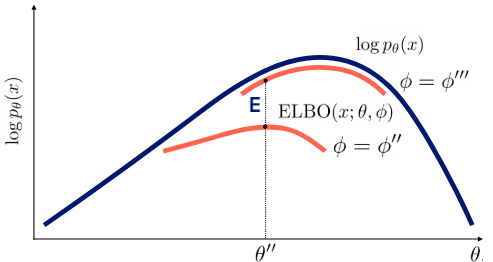
하지만 여기까지 글을 읽을 보면서 이상한 점이 느껴져야 하는데 z의 posterior이 과연 뭐냐는 것이고 계산할 수 있냐는 것이냐이다.

식을 보면 posterior를 알기 위해선 p(x)를 알아야한다.(p(x)가 어려워서 z도입했더니 p(x)를 계산해야 하는 웃픈 상황) p(x)는 매우 복잡한 분포여서 이 식 역시 계산할 수 없으므로 E-M method를 사용하지 못한다.
그래서 사용하는 방법이 variational approximation인데 이 방법은 간단한 parametric distribution으로 근사하는 방법으로 z의 posterior를 가우시안 분포로 근사한다.(q를 구하는 parameters인 파이는 variational parameters라 하고 복잡한 함수를 근사하여 추론하는 것을 variational inference라 한다. 그리고 variational parameters는 당연히 x에 딸라 달라지므로 x에 대한 함수로 볼 수 있다.)
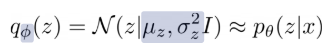
물론 이 발상이 항상 타당한 것은 아니다. 아래 그림에서는 꽤나 괜찮은 근사를 하지만

이 그림에선 매우 poor하다.

다시 그동안 했던 것들을 되돌아보면
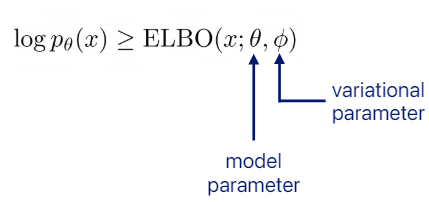
Evidence를 maximize하려던 목표는 ELBO을 maximize하는 것으로 바뀌었고 이는 q(z)와 p(z|x)의 차이를 최소화하는 과정이 필요했으나 불가능하여 variational approximation을 사용한다. 마치

를 하는 것과 같아진 것.
3. Variational Auto-Encoder(VAE)
이번엔 VI를 응용한 신경망인 VAE에 대해 알아보자. VAE는 x를 latent variable z로 encoding하고 이를 다시 decoding하여 x와 유사한 x틸다를 생성하는 것이다. z에 대한 posterior이 아닌 prior를 도입해보자.

여기서 왼쪽 term은 reconstruction term이라 하는데

근사된 z(q(z)의 확률 분포를 갖는 z)에서 x가 잘 re-generate되는지 확인하는 term이다. 값은 당연히 크면 클수록 잘 근사한 것이다.
오른쪽 term은 regularization term인데

근사한 z의 분포가 실제 z의 분포(prior)과 유사해는지 확인하는 term이다. 값이 크면 차이가 큼을 의미하므로 -가 붙는다.
일반적으로 VAE에서 z의 prior는 N(0,1)로 가정한다.
Regularization term을 보면 (생략되었지만 두 분포 모두 given x에서 얻어졌다.) 따라서 variational parameters 역시 VI와 마찬가지로 x에 대한 함수이다. VI에선 언급하지 않았지만 이 부분이 문제가 되는데 그럼 모든 x에 대해서 파이를 계산해야 하는 문제가 생겨 scalable하지 않다.(scalable하다는 것은 많은 양의 x에서도 합리적인 계산이 가능해 확정가능함을 의미한다.)

따라서 VAE에서 도입한 것이 encoder architecture인데 이 구조로 amortized inference가 가능하다.
뭔 소리냐? x를 입력하면 뮤와 시그마를 출력하는 신경망을 만드는 것. 이 신경망 하나를 학습시키면 각 파라미터를 모두 학습시키는 것보다 훨씬 간단해진다.(amortized는 '공통으로, 한꺼번에'를 의미한다.)

이렇게 만든 q(z|x)에서 z를 sampling하고 decoder를 통해 x 틸다를 만들어 낸다.
그럼 실제로 reconstruction term을 어떻게 계산하는지 알아보자.


VAE 역시 신경망이다 보니 differentiable이 필수이다. 하지만 sampling process는 일반적으로 non-differentiable이다. 따라서 우린 reparameterization trick을 통해 이 과정을 미분가능하게 할 것인데 z를
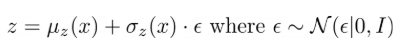
로 sampling하고 gradient를 계산하는 것이다. z의 prior이 N(0,1)으로 unbiased하고 minibatch size가 클 때 이렇게 one sample로 gradient를 계산하여도 동일한 효과를 내는 것은 수학적으로 밝혀져있다.(이부분은... 납득!)
이후 decoder 과정에서 x 틸다를 N(x|x*, I)에서 sampling하는데(시그마를 1로 가정) 이 때

가 성립한다.(x_{rec} = x 틸다)
왜냐하면 가우시안 분포가

이렇게 생겼는데 log를 씌우면

이고 앞 항은 constant여서

이다. 즉, 의미를 분석하면 reconstruction term은 x와 x 틸다 사이의 유클리드 거리의 제곱이 최소화되도록 학습하는 것이다.
이번엔 regularization term을 살펴보자.

p(z)는 일반적으로 N(0,1)로 가정하고 q(z)는 z의 posterior 인데 이 역시 Gaussian distribution이므로 위 식은 closed form이 존재해 생각보다 쉽게 계산된다.
즉, sampling을 포함한 전체 process를 보면

가 된다. 이제 각 term이 어느 층과 연결되는지까지 표현하면

이렇게 되고 역전파를 나타내면
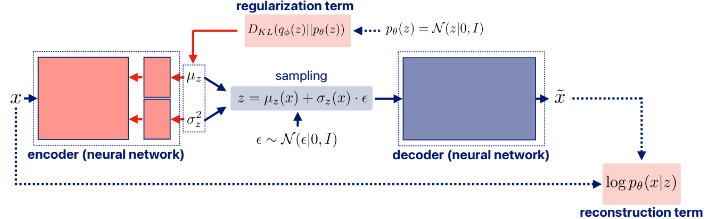
와
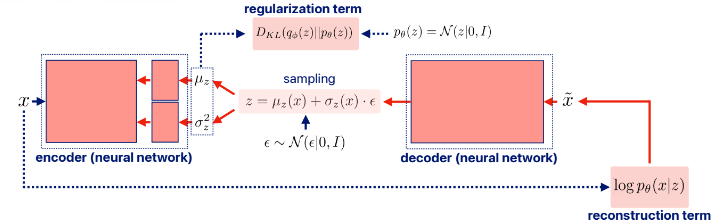
이다. 결론적으로 우리는 latent variable z를 통해 새로운 것을 'generation' 할 수 있게 되었다.

+

이 주석을 봤을 때 의문이 들어야 하는 것이 'x 틸다를 sampling한다.'는 표현이다. 그럼,

이 backporpagation에서 x 틸다는 sampling process를 거치기 때문에 미분이 가능한지 의구심을 들게 만든다.
결론부터 말하면 둘다 맞다.
우선 미분이 가능한 이유는 deocder는 주어진 z에 대해 하나의 결정적인 출력을 만든다. 즉, 주어진 z에 대해 항상 동일한 x 틸다를 생성하는 것이다.(x 틸다 = g(z)) 그럼, sampling 했다고 표현할 수 있는지 생각이 들 수 있는데 x가 잠재 변수 z로부터 생성될 때 가우시안 분포로부터 생성된다고 가정했기 때문에 하나의 sample을 추출한 것으로 해석할 수 있다. 당연히 정규 분포에서 가장 가능성이 높은 평균을 sample하는 것이 자연스럽기 때문에 이 x틸다는 z로부터 출력한 p(x|z_ 분포의 평균이고 이를 통해 reconstruction term을 계산한다.
정리하면 z를 통해 x가 바로 결정되고 x는 p(x|z)에서 하나 sampling 된 것으로 볼 수 있다.
4. Hierachical Variational Auto-Encoder(HVAE)
VAE에서 latent variable이 여러 개로 확장되고 각각이 depencency가 존재하는 모델이 HVAE이다. 이는 diffusion의 기반이 되니 다음 포스트에서 또 언급하겠다.
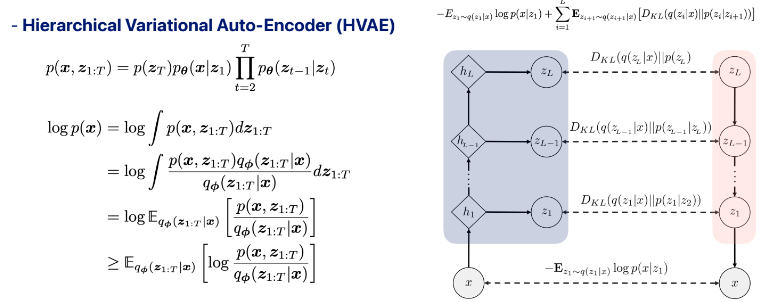
5. Recurrent VAE
VAE를 확장한 또다른 구조로 recurrent VAE가 있다. Hidden variables 사이에 recurrence가 존재하는 것이 특징이다.

6. Problems with VAE
1. inefficient to evaluate / measure the likelihood of observed data
: 애초에 위 과정이 모두 이루어진 것이 p(x|z)p(z)dz가 적분이 되지 않아 이런 먼길을 돌아온 것이다. 적분을 학술이는 방법이 있긴 하지만(MCMC(Markov Chain Monte Carlo) 방법은 복잡한 확률 분포에서 샘플링하여 적분 문제를 해결하는 강력한 수치적 방법) 계산 과정이 매우 많아 비효율적이다.
2. not perfect samples from the distribution
: 1번 때문에 간단한 함수로 근사하는 variational inference를 하지만 '간단한' 함수이기 대문에 생성하는데 완벽하지 않다. 즉 normal distribution으로 복잡한 분포는 근사하기에는 충분하지 않다. 실제로 생성해보면 over smoothing한 x 틸다가 아래처럼 생긴다.

3. posterior collapse with strong decoder
: 만약 decoder가 너무 강하면(capacity가 크다면) 잠재변수 z를 무시하고 그냥 x로부터 x틸다를 구성해버린다. Encoder를 사용하지 않지만 마치 학습되는 것처럼 보이기 대문에 모델의 표현력이 개선되지 않는다.
7. 마무리
이렇게 저번 기말 범위 중 하나였던 VAE에 대한 내용을 마치고 다음 포스트는 HVAE에 제약을 더한 diffusion에 대해 올려보겠다. (지금부터 해야 되긴해..)
'DL > Generative Model' 카테고리의 다른 글
| [Paper Review] Denoising Diffusion Implicit Models (0) | 2024.07.24 |
|---|---|
| CT-GAN, TVAE + CTAB-GAN, CTAB-GAN+ (0) | 2024.07.21 |
| [Paper Review] Denoising Diffusion Probabilistic Models (0) | 2024.07.16 |
| [Paper Review] Auto-Encoding Variational Bayes - VAE (0) | 2024.07.10 |
| [Generative Model 스터디] 1주차-2(DDPM+스터디 preivew 영상) (0) | 2024.07.03 |