원래 autoencoder는 1980년대 만들어진 신경망 모델 중 하나로 데이터를 효율적으로 표현하기 위해서 고안되었다. Encoder 구조를 통해 데이터를 압축하고 decoder 구조로 다시 복원하는 과정을 통해 데이터의 중요한 특징을 추출하는 것이 목표였는데 이 구조를 유지한 채 각각의 목적에 맞게 설계되어 noise를 제거하는 DAE, 새로운 데이터를 생성하는 VAE 등으로 발전하였다.
오늘 다뤄볼 모델은 VAE이다. 참고한 논문은 'Auto-Encoding Variational Bayes' by. Diederik P Kingma, Max Welling이고 아래 사이트에 기재되어있다.
[1312.6114] Auto-Encoding Variational Bayes (arxiv.org)
Auto-Encoding Variational Bayes
How can we perform efficient inference and learning in directed probabilistic models, in the presence of continuous latent variables with intractable posterior distributions, and large datasets? We introduce a stochastic variational inference and learning
arxiv.org
수식은 아래 사이트를 참고하였습니다.
[논문리뷰] Auto-Encoding Variational Bayes(VAE) 모든 수식 알아보기 (tistory.com)
[논문리뷰] Auto-Encoding Variational Bayes(VAE) 모든 수식 알아보기
0. 들어가며 제목은 모든 수식을 알아본다고 호기롭게 썼으나 제가 이해한 만큼만 이 포스팅에 담길 예정입니다. 학습이 어떤식으로 이루어 지는지에 초점을 맞추기 보다는 왜 loss가 이런 식으
rla020.tistory.com
Abstract
- 우리는 어떻게 intractable posterior distributions를 갖는 continuous latent variables가 존재하고 large datasets에서 효율적인 inference와 directed probabilistic models를 학습할 수 있을까?
- by. stochastic variational inference & learning algo.
- 우리는 이 논문을 통해 크게 2가지를 기여함.
- reparameterization of the variational lower bound로 간단한 SGD로 최적화 가능한 a lower bound estimation를 만든 것
- approximate inference model을 proposed lower bound estimator를 통해 intractable posterior에 fitting 시켜 posterior inference가 효율적으로 수행되게 하는 것
1. Introduction
- Directed probabilistic models에서 연속적인 잠재 변수와 파라미터가 intractable(앞으로 '난해한, 복잡한'으로도 자주 쓰겠다.) posterior distributions(p(z|x))를 가지면 어떻게 효율적으로 근사추론하고 학습할 수 있을까?
- variational Bayesian(VB) approach
- 복잡한 사후 분포를 더 간단한 분포로 근사하여 계산의 용이성을 도모하는 접근법
- 기본 아이디어는 근사 분포 선택과 ELBO(Evidence Lower Bound, evidence는 x의 log-likelihood) 최적화로 이루어짐.
- variational은 원함수가 어려울 때 다른 함수로 대체하는 방법을 의미


위 식의 유도과정
- VB의 방법 중 하나인 mean-field접근법이 있는데
- 근사 분포를 각 잠재 변수가 독립적인 형태로 근사해 다변수 분포를 단변수 분포의 곱으로 나타낸다.
-

- mean-field 접근법은 물리학에서 유래되어 복잡한 시스템에서 모든 상호작용을 계산하기 어려워 평균적은 장으로 근사하는 방식임.
- 하지만 이런 가정을 하더라도 general case에서 approximate posterior q(z)는 적분하기 어렵다.(논문에서 말하는 analytical solutions은 수학공식을 통한 적분을 말함.)
- 따라서. variational lower bound를 reparameterization을 통해 simple differentiable unbiased estimator of the lower bound를 만들고 이 SGVB(Stochastic Gradient Variational Bayes) estimator가 efficient approximate posterior inference에 사용됨을 보일 것이다.
- variational Bayesian(VB) approach
- i.i.d. dataset(각 data points 독립적, from 동일한 분포)과 data point마다 continuous latent variable이 있는 경우 Auto-Encoding VB(AEVB) algo. 를 제안한다.
- 이 알고리즘은 SGVB estimator로 inference와 learning을 효율적으로 가능하게 해 recognition model을 최적화할 수 있다.
- 그 결과, simple ancestral sampling(모델의 구조에 따라 순차적으로 sampling 하는 것)으로도 매우 효율적인 approximate posterior inference가 가능하다. -> 빠른 learning으로 이어짐., 비싼 interative infernce(MCMC) 같은 거 안 써도 됨.
- 이런 learned approximate posterior inference model은 다양한 task에도 쓰일 수 있고 특히 neural network와 결합하면 variational auto-encoder가 된다.
2. Method
- 이번 장에선 lower bound estimator(a stochastic objective function)을 유도해 볼 것이다.
- 사전에 하는 가정은 i.i.d dataset with latent variables per datapoint, maximum likelihood(ML) or maximum a poseteriori(MAP)가 목표이고 latent variables에 대해 variational inference를 하는 것이다.
- variational inference: 복잡한 확률 분포를 계산하기 쉬운 분포로 근사하여 접근하는 방법
- 이 시나리오를 글로벌 파라미터에 대해서도 variational inference를 수행하는 경우로 확장하는 것은 간단하다. 해당 알고리즘은 appendix F에 올려두지만 이 경우에 대한 실험은 앞으로 연구가 필요하다.(VAE는 잠재 변수에 대해서만 variational inference를 수행함.)
- 우리의 아이디어는 실시간으로 연속적인 생성과 전달되어 분석 및 처리가 요구되는 streaming data에서도 사용할 수 있지만 간단히 하기 위해 fixed dataset으로 가정하겠다.



- 2.1 Problem scenario
- 우리는 데이터 x가 보이지 않는 continuous random variable z로부터 random process를 통해 만들어졌다고 가정하자.
- 이 프로세스는
- z는 true parameter 세타*로 이루어져 있는 prior distribution p_{세타*}(z)로부터 생성되고
- x가 conditional distribution p_{세타*}(x|z)로부터 만들어진다.
- 이렇게 two steps로 이루어진다.
- p_{세타*}(z), p_{세타*}(x|z)는 각각 parametric families of distributions에서 온다고 가정하는데 이는 각각의 분포가 특정한 parameter를 통해 결정됨을 의미한다.(가우시안이면 평균과 분산)
- p_{세타*}(z), p_{세타*}(x|z)는 세타와 z에 대해 미분 가능도 가정
- 그리고 이러한 과정은 대부분 hidden process이기 때문에 true pparameter 세타*, latent variable z 역시 알지 못한다.
- 매우 중요한 것이, marginal과 posterior에는 simplifying assumptions를 적용하지 않은 것!

prior과 likelihood는 parametric familes에서 오는 반면 marginal과 posterior에는 제약 x - 우리는 다음의 case에서도 작동하는 일반적인 알고리즘에 관심 있다.
- Intractability: marginal likelihood인 p(x)= ∫p(z)p(x|z)dz가 intractable한 상황. 즉, p(x)를 계산할 수 없고 미분할 수 없다. + true posterior density p(z|x) = p(x|z)p(z)/p(x)가 intractable하여 EM algorithm을 사용할 수 없는 상황 + mean-field VB algo.에서 필요한 integrals 역시 intractable한 상황.
- likelihood functions p(x|z)가 적당히 복잡하기만 하더라도 자주 생기는 상황이다.(neural network with nonlinear hidden layer이면 당연)
- EM algo를 사용하려면 p(x)를 알아야 한다.

자세한 내용은 https://go-big-or-go-home.tistory.com/8 에
- A large dataset: 데이터 셋이 많아 모든 데이터를 한꺼번에 처리하는 batch optimzation을 못하기 대문에 minibatches가 single datapoints로 update를 하려 한다. 이때, sampling methods는 각 데이터 포인트 혹인 mini batches마다 반복적으로 sampling을 수행해야 하므로 너무 많은 비용이 든다.
- Intractability: marginal likelihood인 p(x)= ∫p(z)p(x|z)dz가 intractable한 상황. 즉, p(x)를 계산할 수 없고 미분할 수 없다. + true posterior density p(z|x) = p(x|z)p(z)/p(x)가 intractable하여 EM algorithm을 사용할 수 없는 상황 + mean-field VB algo.에서 필요한 integrals 역시 intractable한 상황.
- 우리는 이에 대한 해결책을 제시하기 위해 세 가지 관련된 문제로 쪼갰다.
- Efficient approximate ML or MAP estimation for the parameter theta
- hidden process를 모방하고 real data와 비슷한 데이터를 만들 수 있다.
- Efficient approximate posterior inference of the latent variable z given an observed value x for a choice of parameters theta
- coding or data representation tasks에 적합하다.
- Efficient approximate marginal inference of the varible z
- 여러 방면에 사용된다.(prior of x이니까)
- Efficient approximate ML or MAP estimation for the parameter theta
- 위 문제들을 해결하기 위해 recognition model q_{파이}(z|x)를 도입한다. 이는 intractable true posterior p(z|x)를 근사한 것이다.
- 또한 알아야 할 것이 mean-field variational inference와 다르게 factorial할 필요가 없고(factorial하다는 것은 잠재변수끼리 독립적일 필요가 없다는 것) recognition model의 파라미터 파이는 단순한 수학적 기댓값 공식으로 계산될 필요가 없다.
- 대신 recognition model parameters 파이와 generative model parameters 세타를 동시에 학습하는 learning method를 도입할 것이다.
- Coding theory 관점에서 unobserved variables z는 latent representation or code로 볼 수 있어 recognition model q(z|x)를 확률적 encoder로 볼 수 있다. 주어진 datapoint x에 대해 z에 대한 분포를 만들기 때문.(단, x가 생성될 수 있는 z들로 한정) 같은 관점으로 p(x|z)는 확률적 decoder가 된다. 주어진 code z로 대응되는 x에 대한 분포를 만들기 때문.
- 2.2 The variational bound
- marginal likelihood는 individual data points의 marginal likelihoods의 합으로 구성된다.

- 그리고 이 각 데이터 포인트의 marginal likelihood는 다음과 같이 쓸 수 있다.



(1), (2) 유도 - 우측항의 왼쪽 KL divergence는 true poseterior와 그것의 근사에 대한 차이이고 이 값은 non-negative이기 대문에 두 번째 항은 L(세타, 파이; x)는 (variational) lower bound on the marginal likelihood of datapoint i와 동일하다.
- 이 식은 다시 아래와 같이 쓸 수 있는데


(3) 유도 - 우리는 lower bound를 variational parameters인 파이와 generative parameters 세타로 미분하고 최적화하려 하는데 파이에 대한 미분은 좀 문제가 있다.
- Monte Carlo gradient estimator를 기댓값에 적용한 식은 다음과 같은데

where z^(l) ~ q(x❘x^(l)) 첫번째 term에서 두번째 term으로 넘어가는 부분 스코어함수 트릭인데 확률 분포에 대한 기대값의 그라디어트를 계산하는데 사용된다고 한다. 그라디언트 logq(z)를 score function이라 한다. - 이 값이 매우 높은 분산을 보여 실용적이지 않다는 것이다.(아래 2.4 section에서 reparameterization trick과 score function을 비교해 보겠다.)
- 2.3 The SGVB estimator and AEVB algorithm
- 이번 section에선 실용적인 lower bound estimator랑 그것의 미분된 것을 구해볼 것인데 여기서 사용되는 기법이 posterior을 근사한다고 가정한 q(z|x) 뿐만 아니라 q(z)에도 적용될 수 있다.(변분 추론 기법이 적용 범위가 넓음을 의미)
- section 2.4에서 소개될 조건 하에서 선택된 approximate posterior q(z|x)에 대해 q(z|x)를 따르는 random variable z틸다를 differentiable transformation g(e, x)와 보조 noise variable e를 통해 reparameterize할 수 있다.

- section 2.4에 적절한 분포 p(e)와 함수 g(e, x)를 잡는 법을 소개한다. 우리는 이제 f(z)의 Monte Carlo estimates of expectations을 다음과 같이 계산할 수 있다.

- 이를 eq. (2)에 적용하여 일반적인 Stochastic Gradient Variational Bayes (SGVB) estimator를 얻는다.


시그마 오른쪽의 두 term에 괄호 있어야 한다. - eq.(3)의 KL-divergence D(q(z|x)||p(z))는 주로 적분가능하다.(appendix B에서 볼 거임.) 따라서 오른쪽에 있는 expected reconstruction error E_q[log(p(x|z))]의 sampling만 근사하면 된다. 식의 의미를 살펴보면 KL-divergence term은 approximate posterior를 prior p(z)에 가깝게 하는 파이에 대해 regularizing 하는 term이다. eq. (3)에 reparameterization trick을 사용하면


- 이렇게 두 번째 버전 SGV estimator가 나오고 이 식은 일반적으로 generic estimator보다 작은 분산을 갖는다.
- 왜 그런지에 대한 얘기는 없는데 단순히 z에 의존하는 term이 두 개여서 그런가 싶다...
- data set X가 총 N datapoints가 있다면 minibatches로 전체 marginal likelihood를 다음과 같이 구할 수 있다.

where the minibatch X^M = {x^(i)}(i=1,...,M) is a randomly drawn sample of M datapoints from the full dataset X with N datapoints. - 그럼 Auto-Encoding VB (AEVB) algo. 다음과 같이 구현된다.

- auto-encoders관의 관계는 eq.(7)을 보면 명확하다.
- 첫 번째 term은 KL divergence of the approximate posterior from the prior로 regularizer의 역할을 수행한다.
- 두 번째 term은 expected negative recounstruction term으로 함수 g()는 x와 noise vector e를 approximate posterior에서 뽑은 sample인 z로 mapping해주는 역할이고 그 z가 두번째 term으로 들어간다.
- log(p(x|z))는 under generative model, given z에서 datapoint x의 확률을 의미하는데 당연히 크면 클수록 좋으니 negative가 붙어 negative reconstruction error이다.
- 2.4 The reparameterization trick
- 우리는 문제를 해결하기 위해 q(z|x)에서 샘플을 생성하는 부분을
- score function trick에서

z를 샘플링해 그라디언트 기호 뒤의 log값이 고차원일 때 큰 값을 가진다고 한다. - reparameterization trick으로

noise를 샘플링해 미분가능한 함수로 z를 구하므로 상대적으로 분산이 작다. - 넘어왔다.
- -------------------------------------------------------------------------------------------------------------------------------------------------
- + 이 부분은 논문에 없지만 score function trick과 reparameterization trick의 분산을 비교해 보겠다.
-

score function trick으로 gardient의 분산 samplin 하기 
reparameterization trick으로 gradient의 분산 구하기 
이렇게 score function trick을 사용했을 때 분산이 훨씬 크다. 노이즈가 gardient 추정에 미치는 영향을 줄이기 때문에 안정적인 추정이 가능하게 한다고 한다. - 그럼 왜 높은 분산을 가지면 안 좋은 걸까?
- 높은 분산은 학습에 불리하기 때문. 학습 속도가 느려지고 최적화 과정에서 적절한 방향으로 수렴하지 못할 가능성이 높아짐. 즉 학습이 불안정해지는 것. + overfitting, underfitting 가능성 모두 증가
- -------------------------------------------------------------------------------------------------------------------------------------------------
- 재매개변수화 트릭의 본질은 간단하다. 연속 확률 변수 z가 q(z|x)라는 분포를 다른다고 가정하면 random variable z를 z=g(e, x) 같이 결정론적 변수로 표현할 수 있다.(e는 independent marginal p(e)를 갖는 보조 변수, ㅎ()는 파라미터 파이에 의해 매개변수화된 벡터 함수)
- 이 트릭이 왜 우리에게 유용한가면 이를 통해 q(z|x)의 Monte carlo estimate of the expecation를 미분가능하게 해 주기 때문이다.
- 증명은 z = g(z|x)인 결정론적 mapping이 주어졌을 때
- 확률 분포를 변환하면(이 부분이 잘 이해가 안 갔는데 수리 통계를 공부해야 할 거 같다..)
-

- 가 성립하고
 이어서
이어서 
- 가 성립한다. 2.3에서 이 트릭으로 variational lower bound에 대해 미분가능한 estimator를 얻은 것.
- 몇 가지 예시를 들어보면 만약 z가 단변량 가우시안 분포를 따른다고 하면

- 유효한 reparameterization은 z=μ+σϵ이다.
- 따라서 기댓값이 다음과 같이 변하고
-

-
- 몬테카를로 추정을 하면
-

- 가 된다.
- 이렇게 특정 분포 q(z|x)에 대해 미분 가능한 변화 g(e, x)아 보조 변수 e를 선택할 수 있는 건 다음 3가지 접근 방식 중 하나라도 가능할 때이다.
- Tractable inverse CDF: 만약 q(z|x)의 역 누적 분포 함수를 계산할 수 있는 경우 적용할 수 있다. 이 경우 g(e, x)에서 e는 U[0, I]를 따른다.
- examples: Exponential, Cauchy, Logistic, Rayleigh, Pareto, ...
- Gaussian example과 유사하게 "location-sacle" family of distributions에 해당하는 경우 standard distribution을 따르는 e를 auxiliary variable로 사용할 수 있다.
- examples: Gaussian, Laplcae, Elliptical, Student's t, Logistic, Uniform, ...
- 랜덤 변수를 보조 변수의 다양한 변환으로 표현할 수 있는 경우
- examples: Log-Normal(정규 분포된 변수의 지수 변환), Gamma(지수 분포된 변수들의 합), Dirichlet(감마 변수들의 가중합), Chi-Squared, Beta, ...
- Tractable inverse CDF: 만약 q(z|x)의 역 누적 분포 함수를 계산할 수 있는 경우 적용할 수 있다. 이 경우 g(e, x)에서 e는 U[0, I]를 따른다.
- 이러한 접근법들이 모두 불가능한 경우 inverse CDF에 대한 좋은 근사 방법이 있긴 한데 PDF의 시간 복잡도와 필적한 계산이 든다.
3. Example: Variational Auto-Encoder
- 이번 section에선 probabilistic encoder로 neural network를 사용한 example인 variational auto-encoder에 대해 알아보겠다. parameters 파이와 세타는 AEVB algo.에 의해 jointly optimize된다.
- latent variables의 prior p(z)를 centered isotropic multivariate Gaussian으로 가정한다.(평균이 0이고 공분산 행렬이 단위행렬인 가우시안 분포)

- 이 경우 사전 분포는 파라미터를 가지지 않는다. 평균과 공분산 행렬이 고정되어 있으므로 학습할 파라미터가 없다.
- p(x|z)의 경우 x가 실수값 데이터의 경우 multivariate Gaussian, 이진 데이터의 경우 Bernoulli 분포이다. 이 분포의 파라미터는 MLP(단일 은닉층을 가진 완전 연결 신경망)을 통해 z로부터 계산된다. -> appendix C
- 실제 사후 분포 p(z|x)는 계산하기 어렵다. 반면 이를 근사한 q(z|x)의 형태에는 많은 자유도가 있지만 우리는 실제(계산 불가능하지만) 사후 분포가 대각 공분산을 가진 가우시안 분포를 따른다고 가정한다. 이 경우 variational approximate posterior 역시 대각 공분산 구조를 가진 다변량 가우시안 분포로 설정할 수 있다.

approximate posterior의 평균과 표준편차는 encoding MLP의 출력이다. 이 MLP는 데이터 포인트 x와 variational parameters 파이의 비선형 함수로 평균과 표준편차 계산한다. - 2.4에서 설명했듯이 z를 아래와 같이 sampling한다

e는 N(0, I)를 따르고 원에 중심이 찍힌 기호는 element-wise product를 의미한다. - 이 모델의 경우 p(z) -> prior과 q(z|x)를 Gaussian으로 가정하기 때문에 eq.(7)에 estimator를 사용할 수 있다.(KL-divergence는 근사 없이 계산 가능함! -> appendix B)
- 따라서 data point x와 모델에 대한 최종 estimator는
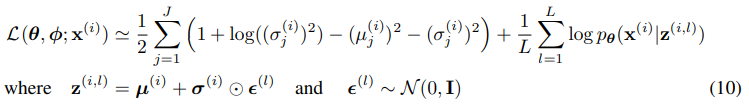
- 와 같다.
- 뒤에 붙는 decoding term log(p(x|z))는 modeling하는 data의 type에 따라 Bernoulli or Gaussian MLP이다.
4. Related Work
- 연속적인 잠재 변수를 사용한 model에 적용 가능한 온라인 학습 방법으로 wake-sleep 알고리즘만이 존재한다.
- 우리의 방법과 마찬가지로 실제 사후 분포를 근사하는 recoginition model을 사용한다.
- wake-sleep algo.의 단점은 두 objective functions를 동시에 근사해야 하는데 두 목표함수가 결합되어 이는 marginal likelihood의 최적화와 다르다는 것이다.
- 장점은 이 알고리즘이 이산 잠재 변수를 포함하는 모델에도 적용될 수 있다는 점이다.
- 데이터 포인트당 계산 복잡도는 AEVB와 동일하다.
- 최근에 stochastic variational inferencec가 주목받고 있다. 최근에 2.1에서 논의된 단순 gradient esstimator의 높은 분산을 줄이기 위해 제어 변수를 도입하였고 이를 exponential family approximations of the posterior에 적용하였다. 좀 더 일반적인 방법으로 이 paper와 유사한 reparameterization이 exponential-family approximating distributions의 natural parameters를 학습하기 위한 stochastic variational inference algo.에 사용되었다.
- AEVB algo.는 directed probabilistic models(trained with a variational objective)와 auto-encoders 사이의 관계를 보여준다. 선형 auto-encoders와 generative linear-Gaussian models 사이의 관계는 오래전부터 알려져 있었다.
- PCA와 사전 분포 p(z) = N(0, I)와 조건부 분포 p(x|z) = N(x:Wz, eI)(특히 e가 매우 작은 경우)를 가지는 특수한 경우의 linear-Gaussian models의 ML의 해와 일치함을 보였다.
- autoencoders에 관한 최근 관련된 연구는 비정규화 오토인코더의 훈련 기준이 입력 X와 잠재 표현 Z 사이의 mutual information의 하한을 최대화하는 것과 일치함을 보여주었다. mutual information을 최대화하는 것은 conditional entropy를 최대화 하는 것과 같으며 이는 autoencoding 모델에서 데이터의 expected loglikelihood(negative reconstrunction error)의 하한이다. 그러나 이런 reconstruction criterion으론 유용한 표현을 학습하기에 충분하지 않다는 것이 알려져 있다. 유용한 표현을 학습하기 위해 정규화 기법이 제안되었으며, 그 예로 denoising , constractive and sparse autoencoder 변형이 있다.
- SGVB objective는 variational bound에 의해 정해지는 regularization term이 포함되어 있으며 이는 유용한 표현을 학습하는데 필요한 일반적인 regularization hyperparameter가 필요하지 않다. Predictive sparse decomposition(PSD)와 같은 encoder-decoder 구조와도 관련이 있으며, 여기서부터 영감을 얻었다. 또한 최근에 도입된 Generative Stochastic Networks와도 관련 있다. 이 네트워크에서는 노이즈가 있는 auto-encoders가 마르코프 체인의 transition operator를 학습하여 data distribution에서 샘플링한다. Deep Boltzmann Machines의 효율적인 학습을 위해 recognition model을 사용한 사례가 있다. 이러한 방법들은 unnormalized model(Boltzman machines같은 undirected models)이나 sparse coding models에 중점을 둔 반면, 우리의 제안된 알고리즘은 일반적인 directed probabilistic models를 학습하는데 중점을 둔다.
- 최근 제안된 DARN method 역시 auto-encoding 구조를 사용하여 directed probabilistic model을 학습하지만 이 방법은 binary latent variables에 제한된다. 더욱 최근에는 auto-encoders와 directed probabilistic models 및 우리가 paper에서 얘기한 reparameterization trick을 사용하는 stochastic variational infernce의 연결에 대해 제시했다. 그들의 연구는 우리와 독립적으로 개발되었으며 AEVB에 대한 추가적인 관점을 제시한다.
5. Experiments
- 우리는 MNIST와 Frey Face 데이터셋의 이미지로 훈련시켰고 variational lower bound과 marginal likelihood의 측면에서 학습 알고리즘을 비교했다.
- section 3에서 설명된 generative model(encoder)와 variatinal approximation(decoder)를 사용했으며 인코더와 디코더는 같은 수의 hidden units를 가진다. Frey Face 데이터는 연속적이기 때문에 Gaussian outputs를 갖는 decoder를 사용했으며 encoder와 동일하지만 디코더의 출력에 sigmoid activation function을 사용하여 평균을 (0, 1)의 범위로 제안했다. 여기서 hidden units는 인코더와 디코더 neural networks의 hidden layer를 나타낸다.
- Frey Face 데이터의 얼굴 이미지의 각 픽셀 값은 0에서 255 사이의 값을 자유롭게 가지지만 MNIST 데이터의 이미지의 각 픽셀 값은 0 or 255 같이 특정 값만 갖는다.
- 파라미터는 algorithm 1. 에서 이야기한 differentiating the lower bound estimator에 의해 계산된 gradients를 쓰는 stochatic gradient ascent로 업데이트되었다. 또한 사전 분포인 p(세타) = N(0, I)에 작은 wieght decay term이 추가되었다. 이 목표를 최적화하는 것은 likelihood gradient가 gradient of the lower bound로 근사되는 approximate MAP estimation을 수행하는 것과 동등하다.
- 우리는 AEVB 알고리즘과 wake-sleep algorithm을 비교했다. wake-sleep 알고리즘과 variational auto-encoder 모두 동일한 encoder( = recognition model)을 사용하였다. 모든 파라미터, variational, generative paramters 모두 N(0, 0.01)에서 random sampling으로 초기화되었다고 MAP를 기준으로 사용하여 jointly stocastically optimize되었다. Stepsizes는 Adagrad로 조정되었으며, Adagrad global stepsize parameters는 초기 몇 번의 반복에서 훈련 세트 성능을 기준으로 {0.01, 0.02, 0.1} 중에서 선택되었다. 미니배치 크기는 M=100으로, 데이터 포인트당 샘플 L=1개를 사용하였다.
- Likelihood lower bound
- 우리는 MNIST의 경우 500개의 hidden units을, Frey Face 데이터셋의 경우 200개의 hidden units를 가지는 generative models(decoders)와 대응되는 encoders(a.k.a recognition models)로 훈련하였다. Frey Face dataset의 경우 상당히 작은 dataset이기 때문에 overfiting을 막기 위해 hidden units의 개수를 줄였다. 선택된 hidden units의 수는 auto-encoders에 대한 기존 문헌을 기반으로 하였으며, 다양한 알고리즘의 상대적인 성능은 이러한 선택에 크게 민감하지 않았다.
- 다음 그림은 lower bounds를 비교한 결과를 알려준다.

하한은 높을 수록 이득이다. - 흥미롭게도, 과도한 잠재 변수가 overfitting을 초래하지 않았으며, 이는 variational bound의 regularizing nautre로 설명된다.
- Marginal likelihood
- 매우 저 차원의 잠재 공간의 경우 learned generative models의 marginal likelihood를 MCMC estimator를 통해 추정할 수 있다.(자세한 내용은 appendix D에) Encoder와 decoder로 neural networks를 사용했으며 이번에는 100 hidden units과 3개의 잠재변수를 사용하였다.(높은 차원의 잠재 공간에서는 추정치가 신뢰할 수 없게 되었다.)
- 다시 한번 MNIST dataset을 사용하였다. AEVB와 Wake-Sleep method를 hybrid Monet Carlo(HMC) sampler를 사용한 Monte Carlo EM(MCEM)과 비교하였다.(자세한 내용은 appendix E에) 우리는 작은 훈련 세트와 큰 훈련 세트 크기에 대해 세 알고리즘의 수렴 속도를 비교했다.
- 결과는 아래 그림에 나와있다.

- Visualization of high-dimensional data
- 만약 저 차원 잠재 공간(ex. 2D)를 선택하면 learned encoders(recognition model)을 통해 high-dimensional data를 low-dimenstional manifold로 project할 수 있다. MNIST와 Frey Face 데이터 셋의 2D latent manifolds 시각화는 appendix A에 있다.
6. Conclusion
- 우리는 연속적인 잠재 변수를 사용한 효율적인 근사 추론을 하는 variational lower bound의 새로운 estimator인 Stochastic Gradient VB(SGBV)를 소개했다.
- 제안된 estimator는 standard stochastic gradient method를 통해 간단히 미분 및 최적화가 가능하다.
- i.i.d. dataset과 continuous latent variables per datapoint의 경우, 우리는 SGVB estimator를 사용하여 근사 추론 모델을 학습하는, 효율적인 추론 및 학습 알고리즘인 Auto-Encoding VB (AEVB)를 소개한다.
- 이론적인 장점은 실험 결과에 반영되었다.
7. Future Work
- SGVB estimator와 AEVB algorithm은 continuous latent variables를 사용하는 거의 모든 inference and learning problem에 적용될 수 있으므로, 미래 연구 방향이 많이 있다.
- AEVB와 jointly 훈련된 encoders와 decoders에 더 깊은 신경망(ex. convolutional networks)를 사용하여 hierachical generative architectures를 학습하는 것
- time-series models(= dynamic Bayesian networks)
- SGVB를 global parameters에 적용
- 복잡한 noise distributions를 학습하는데 유용한 잠재 변수를 가진 supervised model
Appendix
A. Visualisations
SGVB로 학습된 모델의 잠재 공간과 이에 대응하는 observed space의 시각화는 아래 두 그림이다.


B. Solutions of -D(q(z)||p(z)), Gaussian case

Variational lower bound(the objective to be maximized)는 KL term을 포함하는데 이는 종종 analytically 적분 된다.
VAE에서는 prior p(z)를 N(0, I)로 가정하고 posterior approximation q(z|x) 역시 가우시안이기 때문에 위 항이 생각보다 깔끔하게 적분 되는데 식을 전개해 보겠다.





C. MLP's as probabilistic encoders and decoders
VAE에서 신경망은 probabilistic encoders와 decoders로 사용된다. Encoders와 decoders의 선택은 데이터와 모델의 유형에 따라 다양한데 논문에서는 비교적 간단한 신경만인 multi-layered perceptrons(MLPs)를 사용하였다. 인코더로는 가우시안 출력을 가지는 MLP를 사용하였고, 디코더로는 데이터의 유형에 따라 가우시안 또는 베르누이 출력을 가지는 MLP를 사용하였다.
- C.1 Bernoulli MLP as decoder
이 경우 p(x|z)를 z에서 계산된 확률을 갖는 다변량 베르누이 분포로 가정한다. 이는 단일 은닉층을 가진 완전 연결 신경망으로 이루어져 있다.

- C.2 Gaussian MLP as encdoer or decoder
이 경우 인코더와 디코더는 대각 공분산 구조를 가진 다변량 가우시안 분포로 가정한다.

D. Marginal likelihood estimator
우리는 샘플링된 공간(잠재변수 z의 공간)의 차원이 낮은 경우(5차원 이하)와 충분한 샘플이 있는 경우 marginal likelihood에 대한 좋은 estimates를 만드는 marginal likelihood estimator를 유도하였다. p(x,z) = p(x)p(x|z)를 생성 모델이라 하고 given x에 대해 marginal likelihood p(x)를 estimate해보자.
추정 과정은 세 단계로 구성된다.
1. Hybrid Monte Carlo같은 gradient-based MCMC를 사용하여 posterior에서 z 값을 L개 샘플링한다.
2. z samples에 대해 density estimator q(z)를 fit한다.
3. 다시, posterior에서 L개의 값을 샘플링하고 이러한 samples와 잘 학습된 q(z)를 다음 estimator에 대입한다.

E. Monte Carlo EM
Monte Carlo EM algorithm은 인코더를 사용하지 않고 잠재 변수z의 posterior p(z|x)에서 직접 샘플링한다. 이 때 posterior의 gradient를 사용하는데 gradient는 다음과 같다.

Monte Carlo EM은 accpetance rate가 90%가 되도록 자동으로 조정된 stepsize로 10번의 HMC leapfrog 단계를 수행한 후, 획득된 sample을 이용하여 5번의 가중치 업데이트를 수행한다. 모든 알고리즘에서 파라미터는 Adagrad stepsizes(annealing schedule 동반)를 사용하여 update 된다.
Marginal likelihood는 학습 및 테스트 세트의 첫 100개의 데이터 포인트에서 추정되었으며, 각 데이터 포인트에 대해 4번의 리프로그 단계를 사용하여 Hybrid Monte Carlo로 잠재 변수의 posterior에서 50개의 값을 샘플링했다.
F. Full VB
논문에서 설명한 바와 같이, 잠재 변수에 대해서만 수행한 것과는 달리, 파라미터 세타와 잠재 변수 z 모두에 대해 variational inference를 수행할 수 있다. 여기서는 세타에 대한 estimator를 유도하겠다.
알파로 매개변수화된, 위에서 소개한 parameters에 대한 hyperprior p_{알파}(세타)가 있다고 하자. 그럼 marginal likelihood는 다음과 같이 쓸 수 있다.

... 보충 필요
'DL > Generative Model' 카테고리의 다른 글
| [Paper Review] Denoising Diffusion Implicit Models (0) | 2024.07.24 |
|---|---|
| CT-GAN, TVAE + CTAB-GAN, CTAB-GAN+ (0) | 2024.07.21 |
| [Paper Review] Denoising Diffusion Probabilistic Models (0) | 2024.07.16 |
| [Generative Model 스터디] 1주차-2(DDPM+스터디 preivew 영상) (0) | 2024.07.03 |
| [Generative Model 스터디] 1주차-1(VAE) (0) | 2024.07.01 |