이번에 리뷰할 논문은 diffusion model의 기초를 세운 DDPM을 다룬 논문인 'Denoising Diffusion Probabilistic Models'이다. 이 논문 이전에도 diffusion 아이디어는 있었지만 그 과정을 수식적으로 명확히 다루고 품질인 좋은 샘플들을 생성하였으며 학습 안전성을 높혔기 때문에 유명한 논문이다.(이 논문을 기점으로 diffusion model에 관한 관심이 늘어났다.) 읽어보면서 VAE와의 연관성을 생각해보면 p(x)를 다루기 어려워 latent variable을 통해 분포를 예상한다음 새로운 샘플을 생성해내는 것, reparametrization trick이 사용되는 점 등등이 있겠다. 논문은 아래 사이트에 기재되어있다.
https://arxiv.org/abs/2006.11239
Denoising Diffusion Probabilistic Models
We present high quality image synthesis results using diffusion probabilistic models, a class of latent variable models inspired by considerations from nonequilibrium thermodynamics. Our best results are obtained by training on a weighted variational bound
arxiv.org
Abstract
- 우리는 nonequilibrium thermodynamics에서 영감 얻은 diffusion probabilistic models(a class of latent variable models)를 사용하여 높은 품질의 이미지를 생성해냈다.
-> 간단히 찾아보니 nonequilibrium thermodynamics는 비평형 열역학으로 시스템이 평형 상태에 있지 않을 때의 동적 거동을 설명하는 이론이라고 한다. Diffusion의 diffusion process와 reverse diffusion process가 엔트로피의 변화와 유사한 원리를 바탕으로 작동한다고 한다.
- 우리의 가장 좋은 결과는 diffusion probabilistic models와 denoising socre matching with Langevin dynamics 사이의 새로운 연결에 따라 만들어진 weighted variational bound를 training함으로써 얻어냈다.
- 또한 우리의 모델은 progressive lossy decompression scheme을 허용하며, 이는 autoregressive decoding의 일반화로 해석될 수 있다.
-> Progressive lossy decompression scheme은 여러 단계에 걸쳐서 압축된 데이터를 복원하는 구조를 말하고(손실은 압축시 일부 정보가 사라질 수 있음을 의미, decompression은 압축된 데이터를 다시 원래 상태로 복원하는 과정) autoregressive decoding은 데이터를 순차적으로 예측하며 생성하는 방식이다. Autoregressive decoding의 핵심 아이디어를 포함하면서도, 더 넓은 범위의 문제를 해결할 수 있어 일반화라는 표현을 사용.
- unconditional CIFAR 10 dataset에서 우리는 9.46의 Inception 점수와 3.17의 sota FID 점수를 얻었다.
-> Inception 점수: 생성된 이미지가 얼마나 다양하고, 또 얼마나 실제 데이터와 유사한지 평가하는 지표, 높을수록 생성된 이미지가 다양하고 높은 품질을 가짐을 의미
-> FID 점수: 생성된 이미지와 실제 이미지 분포 차이를 측정하는 지표, 낮을수록 생성된 이미지가 실제 이미지와 매우 유사하며, 높은 품질을 가짐을 의미
-> unconditional은 클래스 레이블 정보를 사용하지 않고 이미지를 생성하는 것을 의미한다.
- 256x256 LSUN에서는 ProgressiveGan과 유사한 샘플 품질을 얻었다.
1. Introduction
- 딥러닝을 사용하는 generative models는 다양한 data 종류에 대해서 좋은 퀄리티의 samples를 만들어냈다.
- 이 논문은 diffusion probabilistic models의 progress를 제안한다. Diffusion probabilistic model은 매개변수화된 Markov chain으로 유한 시간내에 data에 대응되는 samples를 생성하기 위해 variational inference를 사용한다.

- 위 그림에서 q로 표현된 markov chain이 diffusion process로 noise를 추가하는 forward process임. p로 표현된 markov chain은 sampling process로 noise를 제거하는 denoising과정으로 reverse process임. DDPM은 p로 표현된 sampling process를 학습함.(q는 가정하기 때문에 학습하지 않음.)
- 만약 이렇게 추가하는 noise가 작은 양의 Gaussian noise라면 sampling chain의 transitions은 conditional Gaussian으로 표현하기에 충분함. -> 따라서, 간단히 신경망으로 평균과 분산만 예측하면 됨.
- Diffusion model는 정의하기 쉽고 훈련 효율도 높지만 지금까지 고품질 샘플을 생성할 수 있다는 증거가 없었다. 우리는 diffusio models도 좋은 품질의 samples를 만들 수 있음을 보였고 때로는 다른 유형의 생성 모델에서 발표된 결과보다 더 나은 성과를 보이기도 함.
- 추가로 이러한 매개변수화가 denoising score matching over multiple noise levels during traings와 annealed Langevin dynamics during sampling이 동일함을 보여줌.
-> denoising score matching: during traing: 데이터의 확률 밀도 함수를 추정하기 위한 방법으로, 데이터 포인트 주변의 확률 밀도의 기울기를 학습함. Denoising score matching에서는 노이즈가 추가된 데이터에 대해 스코어(확률 밀도 함수의 로그에 대한 기울기)를 추정하고 이를 통해 원래의 데이터 분포를 복원함.
-> annealed Langevin dynamics during sampling: 여러 단계에 걸쳐 노이즈를 점진적으로 줄여가며 데이터 샘플을 생성하는 방법. 각 단계는 앞 단계에서 학습된 스코어(확률 밀도 함수의 로그에 대한 기울기)를 이용하여 노이즈를 제거하고, 점차적으로 더 깨끗한 샘플을 만듦.
-> 두 방식 모두 데이터의 노이즈를 제거하고 원래의 데이터를 복원하는 것인데 본질적으로 같은 원리를 따을 논문에서 보인 것
- 우리의 모델은 다른 likelihood-based models에 비해 경쟁력 있는 log likelihoods를 가지지 못했는데 그 이유는 lossless codelength의 대부분이 사람이 인식할 수 없는 image의 세부적인 부분을 설명하는데 사용되고 있었기 때문이다. 이 현상을 손실 압축의 관점에서 분석해 개선하였다. 확산 모델의 sampling 과정은 progressive decoding의 한 유형으로 autoregressive decoding과 유사하지만, 더 일반화된 방식으로 작동하였다.
-> lossless codelength: 데이터를 압축할 때 손실 없이 필요한 비트 수
-> 손실 압축 관점은 데이터를 완벽히 복원하지 않아도 되지만, 중요한 정보는 남겨두는 방식이기 때문에 사람이 인식할 수 없는 세부사항을 생락하거나 덜 정확하게 표현하는 것. => 효율적이고 효과적인 모델
-> 그 결과 만들어진 것이 progressive decoding(이미지를 한 번에 새엉하는 대신 여러 단계에 걸쳐 점진적으로 만들어나가는 방식)이고 이는 데이터를 한 번에 하나씩 순차적으로 생성하는 방식인 autoregressive decoding보다 일반화된, 유연한 방식임.
2. Background
- 일단 가장 중요한 거

학습하려는 대상이 p가 아닌 q라는 점. VAE랑 또 다르다. 또한 왜 diffusion이 noising인지 단어의 의미로 해석해보면 데이터의 정보가 점점 퍼져서(확산되어서) 노이즈로 가득 차게 되는 것을 표현하기 위함이라 한다.
- Diffusion models은 latent variable model로 p(x_0)는 다음과 같이 형성된다.


- 그런데 여기서 알아야 할 것이 이 x_1, ... x_t인 latents가 모두 x_0와 같은 차원이라는 것이다. -> VAE와 다른 점.
- x_0는 q(x_0)를 따른다.

- x_T는 Gaussian 분포를 따른다.

- reverse process: p(X_T)로 시작하는 학습되는 Gaussian trainsitions으로 이루어진 Markov chain

- forward process: 데이터에 가우시안 노이즈를 추가하는 과정으로 x_0에서 schedule된 베타들로 노이즈들이 추가된다.

사실 베타들은 reparameterization으로 학습해도 되고 그냥 상수로 둬도 된다. 베타 값들은 크기가 작은데 그 이유가 베타가 작은 경우 p와 q가 유사한 함수 형태를 갖기 때문에 reverse process의 표현력이 증가하기 때문이다.
또한 forward process의 놀라운 성질은 x_t를 t에 관계 없이 x_0로부터 closed form으로 샘플링할 수 있다는 점이다.


위 두 표현으로 q(x_t|x_0)를 다음과 같이 쓸 수 있다.

-> 위 과정이 왜 놀랍냐면 sampling process를 매우 단축시킬 수 있기 때문이다.(reparameterization trick을 쓰면 하나의 noise를 샘플링하면 끝임)
- training은 negative log likelihood의 variational bound를 optimizing하는 것이 목표이다.

- 효율적인 학습을 위해 L을 다시 써서 variance를 낮추면 아래와 같은 식이 된다.(왜 variane가 낮고 아래 식이 유도되는 지는 appendix B에 첨부하겠다.)

위 식에서 처음 보는 term이 가운데 term인데 이 term은 p(x_{t-1}|x_t)와 q(x_{t-1}|x_t, x_0) -> forward process posteriors를 비교하는 KL divergence term이다. 갑자기 forward process의 분포에 given x_0가 생겼는데 이는 위의 L의 variance를 낮추는 과정에서 생긴 것이다.(이렇게 초기 추정량에 조건부 기댓값을 추가하여 분산을 낮추는 방법을 Rao-Blackwellization이라 한다.) 이 분포는 아래와 같이 정의되고

모든 term들이 gaussian을 다루거나 gaussian 사이의 KL-divergence를 구하기 때문에 closed form을 갖는다.
3. Diffusion models and denoising autoencoders
- Diffusion models은 마치 제한된 형태의 잠재 변수 모델처럼 보일 수 있지만, 구현에 있어 많은 자유도를 허용함.
-> forward process의 분산인 베타
-> reverse process의 모델 architecture, gaussian distribution parameters
을 선택해야함.
3.1 Forward process and L_T
- 베타 역시 reparameterization으로 학습될 수 있지만 여기선 constants로 고정함. 따라서 q에서 학습될 파라미터가 없기 때문에 식 (5)에서 L_T는 무시함.(p(x_T)도 학습할 거 없으니까)
3.2 Reverse process and L_{1:T-1}
- 먼저 p(x_{t-1}|x_t)(1<t<=T)에서 평균과 분산을 어떻게 고를지 생각해보자.

분산은 학습되지 않지만 시간에 따라 다른 상수로 정하였는데

시그마의 후보론

가 있다. 첫번째 선택은 x_0가 정규분포 N(0,I)를 따를 때 최적이고 두 번째 선택은 x_0가 한 점으로 정해질 때 최적이다.
-> 이미지로 생각하면 x_0의 각 픽셀이 독립적으로 평균 0, 분산 1을 갖는 정규 분포를 따를 때 최적(다양한 이미지가 균일하게 분포되어 있을 때), x_0의 각 픽셀이 고정된 값을 갖는 것을 의미한다.(모든 이미지가 거의 동일한 구조와 패턴을 가지는 경우)
-> coordinatewise unit variance를 갖는 data의 reverse process entropy의 상한과 하한에 대응된다.
분산을 위와 같이 잡아 reverse process의 분포가 다음과 같이 변하면

L_{t-1}을 아래와 같이 쓸 수 있다.

이 식은 당연히 최소화해야 하기 때문에 가장 간단한 접근은 forward process posterior의 평균으로 뮤(x_t,t)를 잡는 것이다.

위 식에서 reparameterization을 통해

에서 x_0를 얻고

를 (8)에 대입하면

를 얻게 된다.
이 식에서 알 수 있는건 forward process posterior의 평균이

으로 표현할 수 있어서 µ(x_t,t)를 아래와 같이 잡는 것이다.

e(x_t)는 아래 x_t의 e를 예측하기 위해

모델이 학습하여 예측하려는 노이즈 추정량이다.
그럼 reverse process에 x_{t-1}을 sampling하는 것은

reparameterization trick으로

을 계산하는 것과 같다.
예측한 평균인 (11)을 (10)에 넣으면

가 된다.
-> 이 식이 denoising score matching과 비슷하고, Langevin-like reverse process의 variational bound와 같아 둘이 동듬함을 보였다고 한다.
- 전체 알고리즘은 다음과 같다.

-> Training 과정에서 t를 sampling하여 접근하는 방식은 계산의 효율성을 높이고 다양한 노이즈 수준을 균형 있게 학습할 수 있게 한다.
+ Diffusion 모델은 다양한 수준의 noise를 학습하기 위해 시간 term을 sampling하고 특정 시간 단계 t에서도 다양한 노이즈에 대해 학습하기 위해 e를 sampling함. 모델은 주어진 x_t와 시간 t를 입력 받아 해당 시점의 노이즈를 e를 예측하도록 학습됨. 이렇게 충분한 훈련이 되면 x_t와 t를 입력받아 노이즈를 예측하고 예측된 노이즈를 사용하여 현재 이미지에서 노이즈를 제거해 x_{t-1}을 계산한다. 이 과정을 무수히 반복해 원본 이미지와 같은 수준의 이미지를 생성해감.
- 요약하자면, rever process의 mean function approximator인 µθ를 예측하도록 학습할 수 있고, 또는 매개변수를 수정하여 ε을 예측하도록 학습할 수 있음.(x_0를 예측하게 할 수도 있으나 초기 실험에서 이것이 더 낮은 품질을 생성함.) ε-prediction parameterization이 Langevin dynamics와 denoising score matching과 유사한 것을 최적화 하는 것이 목표로 하는 단순한 diffusion model의 variational bound 둘과 유사함을 보였다. 그럼에도 불구하고 이것은 단지 pθ(xt−1∣xt)의 또 다른 매개변수화일 뿐이므로, 4장에서 을 예측하는 것과 μt를 예측하는 것을 비교하는 실험을 통해 그 효과를 검증함.
-> ablation study: 모델의 특정 부분을 제거하거나 변경하여 성능을 비교하는 방법
3.3 Data scaling, reverse process decoder, and L_0
- 우리는 이미지 데이터를 픽셀 단위로 scaling해서 [0, 255]를 [-1,1]로 linearly scaling해줌.(시작이 표준 정규분포이니 신경망은 모든 데이터 포인트를 동일한 범위에서 처리하게 됨.)
- discrete log likelihoods를 얻기 위해 마지막 항을 독립된 이산 디코더로 설정함. 이는

이 가우시안 분포로부터 유도된 것으로

왜 이런 짓을 하냐면 애초에 이미지 데이터는 이산 데이터이기 때문. 연속적인 분포를 사용하여 이산 데이터의 로그 우도를 계산하려면 이렇게 이산 값에 따른 정해진 부분을 적분하여 이산값에 대한 확률을 계산해야 함.
-> 이렇게 하면 추가적인 노이즈를 넣거나 복잡한 수학 연산을 할 필요 없이 variational bound와 lossless codelength of discrete data가 같다고 알려져있다고 한.
-> 마지막 x_0를 구할 때는 노이즈를 넣지 않음.

3.4 Simplified training objective
- 3.1과 3.2, 3.3으로 구성한 variational bound는 세타에 대해 미분 가능해 training을 쓰일 수 있다. 그런데 여기서 기존 variational bound를 대신할 수 있는 간소화된 손실 함수를 사용할 것을 주장하는데 식은 다음과 같다.
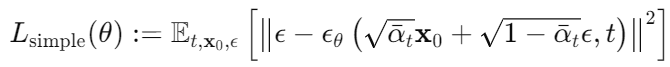
t=1일 때 위 식은 L_0에 대응되는데 (13)에서 정의한 discrete decoder definition의 적분이 gaussian probability density funtion과 bin width를 곱한 것으로 근사된다.(시그마 제곱과 edge effects 무시)
t>1일 때 위 식은 L_1,...,L_t-1이 대응 되는데 (12) 가중치 없는 버전으로 NCSN denoising score matching과 유사하다 한다.
이 식은 표준 변분 경계와 비교했을 때 작은 t에 해당하는 손실 항목의 가중치를 낮추는 역할임. 따라서 네트워크가 더 큰 t값에서 더 어려운 노이즈 제거 작업에 집중할 수 있게 하고 이는 실제 샘플 품질을 높이는 것으로 이어졌다고 함.
4. Experiments
- 모든 실험에 T를 1000으로 맞춤
- 순방향 과정의 분산을 β_1 = 10^-4, β_T = 0.02로 선형 증가하는 상수로 설정함.
-> β 스케줄링 방법에는 여러가지가 있음
1. 선형 스케줄링 (Linear Scheduling)
: β를 일정하게 증가시키는 방법

2. 제곱 스케줄링 (Quadratic Scheduling)
: β 값을 제곱 함수 형태로 증가시키는 방법, 초반과 후반의 차이를 더 극대화

3. 코사인 스케줄링(cosine scheduling)
: α_t를 코사인 함수로 정의하고 β_t 값을 유도하는 방식

-> β들이 [-1,1]로 스케일된 데이터에 비해 작게 설정되어 reverse process와 forward process가 대략 같은 함수 형태를 유지하게 하면서 신호 대 잡음 비율을 가능한한 작게 유지하려 함.(L_T=D(q(x_T|x_0) || N(0, I))≈10^-5 bits per dimension, L_T가 실제 신호 대 잡음 비율을 의미하는 것은 아니지만 L_T가 작게 하면 신호 대 잡음 비율이 줄어듬.)
- reverse process를 나타내기 위해 그룹 정규화(배치 정규화와 유사하지만, 미니배치의 크기에 의존하지 않는 정규화기법, 채널을 여러 그룹으로 나누어 각 그룹 내에서 정규화를 수행한다.)를 전체적으로 사용하는 PixelCNN++과 유사한 U-Net backbone 구조를 가짐. 파라미터는 시간에 걸쳐 공유되며, Transformer 모델에서 사용하는 사인파 위치 인코딩을 적용하여 각 시간 단계에 맞는 위치 정보를 제공함. 또한 16*16 크기의 feature map에서 self-attention mechanism을 사용하여 중요한 부분에 집중할 수 있게 함.
4.1 Sample quality
- 아래 Table 1은 CIFAR10에 대해 Inception scores, FID scores, negative log likelihoods(lossless codelengths)을 기록해놓았다. FID score이 3.17로 우리의 uncoditional model은 알려진 대부분의 model보다 좋은 sample quality룰 보였다. 테스트 세트를 기준으로 계산한 FID score는 5.24로 알려진 다른 모델들의 test set FID score보다 좋다.

- 위 표를 보면 simplified objective로 구할 때보다 true variational bound로 구할 때 더 좋은 codelengths(작을수록 이득임.)를 보였는데 후자가 더 좋은 sample quality(큰 IS, 작은 FID)를 보였다.


다음은 실제로 만든 이미지들


4.2 Reverse process parameteriation and training objective ablation
- 아래 Table 2는 reverse process parameterization과 training objectives의 sample quality effects를 보여줌.

- 우리는 µ를 예측하는 방식은 true variational bound를 구할 때만 잘 작동하는 것을 확인함.
- 또한 reverse process의 variances를 학습하는 것도 실험해보았지만 고정 분산과 비교했을 때 불안정한 학습과 더 낮은 샘플 품질을 초래함.
- ε를 예측하는 방식은 고정 분산으로 variational bound를 사용하여 학습했을 때는 µ를 예측하는 것과 거의 동일하게 수행되었지만, simplified objecive로 학습한 경우 훨씬 더 잘 수행됨.
4.3 Progressive decoding
- Table 1에 CIFAR 10 model의 codelengths도 보여주는데 train과 test 사이의 gap이 최대 0.03 bits per dimension이므로 이는 다른 model에서 보고된 차이보다 적은 차이로 우리의 diffusion model이 overfitting되지 않았음을 나타냄.
- 하지만 여전히 우리의 lossless codelengths는 energy based models와 score matching에서 보고된 큰 추정치보단 좋지만, 다른 유형의 likelihood-based generative models와 비교할 때는 경쟁력이 없음.
-> 우리의 샘플들이 높은 품질을 유지하고 있음에도 불구하고 우리는 diffusion models이 lossy compression에서 높은 품질의 샘플을 생성할 수 있는 inductive bias를 가지고 있다고 판단함.
-> L_1+...+L_T를 rate, L_0를 distortion으로 보면 rate는 1.78 bits/dim이고 distortion은 1.97bits/dim임.(둘이 더해서 3.75)

-> 그런데 이 1.97 비트/차원은 원래 픽셀 값이 [0, 255]로 변환했을 때 RMSE가 0.95에 해당하는 매우 작은 값임.
즉, 절반이 넘는 lossless codelength가 지각할 수 없는 distortions를 설명하는 것임.
Progressive lossy compression
- 우리는 progressive lossy code를 도입하여 이 rate-distortion behavior를 더 탐구할 수 있는데 이 부분은 어려워서 생략...


아무튼 결론은 bits의 대부분이 impreceptible distortions를 설명하고 있다는 거임.
Progressive generation
- 이번엔 아래 식을 통해 각 reverse process에서 x_0를 예측해봄.

이 때 아래 그림처럼 대규모 이미지 특징이 먼저 나타나고 세부 사항은 나중에 나타남.

아래 그림은 다양한 t에 대해 x_t(4개 중 오른쪽 아)가 고정된 상태에서 x_0(가장 오른쪽 아래 사진)를 예측한 결과를 보여줌. t가 작을 때는 거의 모든 것이 보존되고 t가 클 때는 대규모 특징만 보존됨.
-> conceptual compression의 hints가 된다 하는데 conceptual compression은 중요한 대규모 특징을 먼저 보존하고, 세부 사항을 나중에 보존하는 방식임.

Connection to autoregressive decoding
- variational bound를 아래와 같이 다르게 쓸 수 있는데

만약 diffusion process length T가 data의 dimensionality라 하고 forward process q(x_t|x_0)를 t번째 좌표를 만들어내는 것 같이 조건들을 설정해주면 여기서 p_θ를 훈련하는 것이 마치 autoregressive model이 됨.
-> 이 때문에 Gaussian diffusion model을 autoregressive model의 일반화라 볼 수 있음.
4.4 interpolation
- 우리는 stochastic encoder q를 사용하여 x_0, x_0'을 interpolate할 수 있음. q를 사용하여 x_t와 x_t'으로 변환한 후 선형 보간으로 새로운 벡터를 만든 다음 reverse process를 통해 이미지 공간으로 decoding 하는 것임.

즉, 아래와 같이 decoding하는 것.


이는 위 그림의 왼쪽에 모사된 것처럼, 소스 이미지의 손상된 버전을 선형 보간 후 reverse process를 통해 인위적인 흔적을 제거하는 효과를 가짐.
오른쪽 그림은 노이즈를 고정한 채 람다를 달리하면서 보간 및 복원을 보여주는 데 높은 품질의 복원을 생성하며, 포즈, 피부, 톤, 헤어스타일, 표정 및 배경과 같은 속성이 부드럽게 변하는 그럴듯한 보간을 생성하지만 안경은 그렇지 않음.
5. Related Work
- 확산 모델은 흐름(flow) [9, 46, 10, 32, 5, 16, 23]과 VAE [33, 47, 37]와 비슷할 수 있지만, 확산 모델은 q에 매개변수가 없고 최상위 잠재 변수 x_T가 데이터 x_0와 거의 제로의 상호 정보를 가지도록 설계되었다. 우리의 ϵ-예측 역방향 과정 매개변수화는 확산 모델과 여러 노이즈 수준에서의 denoising score matching과 annealed Langevin dynamics를 통한 샘플링 사이의 연결을 확립한다 [55, 56]. 그러나 확산 모델은 간단한 로그 가능도 평가를 허용하고, 학습 절차는 변분 추론을 사용하여 Langevin dynamics 샘플러를 명시적으로 학습한다 이 연결은 또한 특정 가중 형태의 denoising score matching이 Langevin-like 샘플러를 학습하기 위한 변분 추론과 동일하다는 역방향 의미도 가진다. 마코프 연쇄의 전이 연산자를 학습하는 다른 방법들로는 infusion training [2], variational walkback [15], generative stochastic networks [1], 그리고 기타 [50, 54, 36, 42, 35, 65]가 있다.
- Score matching과 에너지 기반 모델링의 알려진 연결에 의해, 우리의 작업은 에너지 기반 모델에 대한 최근 연구 [67–69, 12, 70, 13, 11, 41, 17, 8]에 영향을 미칠 수 있다. 우리의 비율-왜곡 곡선은 하나의 변분 경계 평가에서 시간에 걸쳐 계산되며, 이는 annealed importance sampling의 한 번의 실행에서 왜곡 페널티에 대한 비율-왜곡 곡선을 계산하는 방법을 연상시킨다 [24]. 우리의 점진적 디코딩 논증은 convolutional DRAW 및 관련 모델 [18, 40]에서 볼 수 있으며, 오토회귀 모델 [38, 64]에 대한 더 일반적인 설계 또는 샘플링 전략으로 이어질 수도 있다.
6. Conclusion
우리는 diffusion models를 사용하여 높은 품질의 이미지 샘플을 제시했으며 diffusion models과 variational inference를 통한 Markov chains training, denoising score matching과 Langevin dynamics(이를 확장한 에너지 기반 모델), autoregressive models, progressive lossy compression 간의 연결을 발견했따. Diffusion models이 이미지 데이터에 대해 뛰어난 inductive bias를 가지고 있는 것 같으므로 이 모델이 다른 데이터 형태에서도 유용한지, 다른 유형의 생성 모델 및 머신 러닝 시스템의 구성 요소로서 어떻게 활용될 수 있는지 조사해보고자 한다.
Broader Impact
- 우리의 확산 모델 연구는 기존의 다른 유형의 딥 생성 모델에 대한 연구와 유사한 범위를 갖는다. 예를 들어, GAN, 흐름, 오토회귀 모델 등의 샘플 품질을 개선하려는 노력이 그렇다. 이 논문은 확산 모델을 이러한 기법들의 범주 내에서 일반적으로 유용한 도구로 만드는 데 기여하며, 이는 생성 모델들이 세상에 미친(그리고 앞으로 미칠) 영향을 확대하는 데 기여할 수 있다.
- 불행히도, 생성 모델의 악의적인 사용은 많이 알려져 있다. 샘플 생성 기술은 정치적 목적으로 고위 인물들의 가짜 이미지와 비디오를 생성하는 데 사용될 수 있다. 소프트웨어 도구가 등장하기 전에도 수작업으로 가짜 이미지를 만드는 일이 있었지만, 생성 모델과 같은 도구는 이 과정을 더 쉽게 만든다. 다행히도, 현재 CNN이 생성한 이미지에는 미묘한 결함이 있어 이를 감지할 수 있지만, 생성 모델의 발전은 이를 더 어렵게 만들 수 있다. 또한, 생성 모델은 훈련된 데이터셋의 편향을 반영힌다. 많은 대규모 데이터셋이 인터넷에서 자동화된 시스템에 의해 수집되기 때문에, 특히 이미지가 라벨링되지 않은 경우 이러한 편향을 제거하기가 어렵다. 이러한 데이터셋을 기반으로 훈련된 생성 모델의 샘플이 인터넷에 확산되면, 이러한 편향은 더욱 강화될 것이다.
- 반면에, 확산 모델은 데이터 압축에 유용할 수 있다. 데이터가 더 높은 해상도를 가지게 되고 글로벌 인터넷 트래픽이 증가함에 따라, 이는 인터넷 접근성을 넓은 대중에게 보장하기 위해 중요할 수 있다. 우리의 연구는 이미지 분류부터 강화 학습에 이르는 다양한 다운스트림 작업을 위한 라벨이 없는 원시 데이터에 대한 표현 학습에 기여할 수 있으며, 확산 모델은 예술, 사진, 음악에서 창의적인 용도로도 사용될 수 있다.
'DL > Generative Model' 카테고리의 다른 글
| [Paper Review] Denoising Diffusion Implicit Models (0) | 2024.07.24 |
|---|---|
| CT-GAN, TVAE + CTAB-GAN, CTAB-GAN+ (0) | 2024.07.21 |
| [Paper Review] Auto-Encoding Variational Bayes - VAE (0) | 2024.07.10 |
| [Generative Model 스터디] 1주차-2(DDPM+스터디 preivew 영상) (0) | 2024.07.03 |
| [Generative Model 스터디] 1주차-1(VAE) (0) | 2024.07.01 |