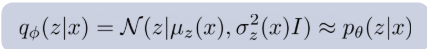다양하지만 얕지 않게

 이번엔 Diffusion Model 중 하나인 DDPM에 대해 알아보자.

2. MLDL2 수업 - Diffusion Models

**무단 배포 금지** 본 게시물의 저작권은 김태섭 교수님께 있습니다.

1. VAE to Diffusion Models

사실 교수님께서 diffusion을 알기 위해선 VAE가 필수라고 하셔서 VAE를 짚고 넘어가는 거긴함.

Diffusion 출발은 저번 포스트의 마지막인 Hierachical Variational Auto-Encoder(HVAE)이다.(이말이 꼭 HVAE를 기반으로 diffusion이 만들었다는 말은 아니고 이해하는 관점에서 HVAE와 비교하면서 보는 것이 타당하다.)

 HVAE는 VAE를 generalize한 모델이다. 기존에 VAE에선 latent variable이 하나였지만 이 variables를 늘리고 이 들을 hierachical하게 설계하여 일반화한 것이다. Hierachical하게 설계했다는 것은 latent variable사이 순서, 계층 구조가 있음을 의미한다. 따라서 latent variable역시 더 높은 level = 더 abstract한 latent variable로부터 생성된다. 

 HVAE에선 abstract할 수록, higher-level로 갈수록 그 크기가 줄어든다. = compact해진다.(encoder에서 출력하는 다음 층의 평균과 분산이 계속 줄어드는 것)

그리고 joint-distribution에 하나의 성질이 있는데 markov property이다. 즉, 다음 요소를 결정하는 것은 바로 이전의 요소만이라는 것.(만약 이 성질이 없다면 저 수많은 latent variable로부터 계산할 수 없을 것이다..)

 마찬가지로 HVAE에서의 encoder는 x로부터 low-level, high-level의 z를 만들어내고

이 역시 markov property를 가지며 이 q(z_{1:T}|x)는 p(z_{1:T}|x)를 추정하는 분포이다.

 HVAE에서 evidence를 써보면 다음과 같이 전개되는데

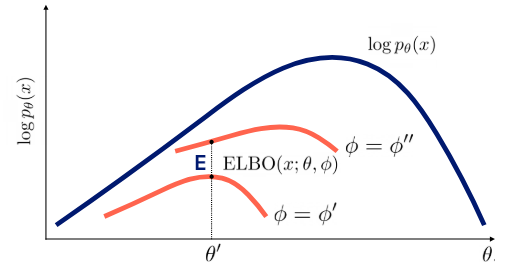
 ELBO에 위 두 그림에서 얻은 식을 넣으면 최종 식이 나오게 된다.

 2. Denoising Diffusion Probabilistic Models(DDPM)

  DDPM은 diffusion model의 초기 model로 VAE에 추가적인 3가지 restrictions를 넣는다.

(수업 자료에는 VDM으로 명시하였는데 나는 틀렸다고 생각한다. VDM은 DDPM과 VAE를 결합한 것이기 때문에 잠재 공간에 대한 이야기가 다루어져야 하는데 전혀 다루지 않기 때문이다. 생각해보면 이런 제약을 넣는 것 자체가 더 기초적인 모델임을 의미한다. 즉 VDM은 아래에서 설명하는 첫번째 제약이 없어지기 때문에 잠재 공간에 대한 자유성이 부여되는 한 단계 더 발전한 모델인 것이다. 더 공부해보고 혹시 내 생각이 틀렸다면 수정하겠다.)

(VAE와 DDPM의 공통점은 간단한 분포로 근사해서 생각하는 variational inference, VI를 한다는 것인데 다루는 공간이 각각 latent space, data space자체를 다루는 것이 차이이다.)

 첫번째가 latent variable의 size와 input data의 size가 갖다는 것인데 위의 HVAE에서 higher-level일수록 compact해진다는 특성이 있지만 VDM에서는 모든 latent variable과 input의 size가 같다.

 두번째는 encoder는 학습되지 않고 pre-defined된 linear Gaussian Model를 사용한다.

 여기서 알파는 hyperparameter이다.

 세번째로 위 gaussian parameters인 알파가 위치에 따라(t로 표현해 시간에 따라가 맞는 표현일 수 있다.) 다르고 마지막 latent variabel x_{T}의 분포는 standard Gaussian N(0,I)이라는 것이다.

 그럼 forward diffusion process는

 이 식을 통해 진행되며 이미지에 noise가 첨가되기 때문에 

 encoding 과정을 noising이라고도 부른다.

 + 왜 정규분포가 저렇게 생겼는가?

 일단 정규분포를 사용하는 이유는 정규분포를 다르는 noise를 넣기 위함이고 그럼 위 식에 의해

 이렇게 다음 단계의 latent variable이 생성된다.(VAE에서 reparameterization trick과 동일한데 사실 꼭 이 방법을 사용하지 않아도 된다. 미분 가능하면서 sampling과 같은 효과를 내는 방식이 또 있다는 뜻) 이 때 앞 계수들의 의해 x_{t}의 분산이 x_{t-1}과 같아지게 된다.

 반대로 reverse denoising process는 생성하는 과정으로

 이 과정을 아래의 식으로 하기 때문에

 평균과 분산을 출력할 network 학습이 필요하다.

 정리해보면

이러한 과정이고

 원 data로 부터 잠재변수의 분포를 추론해가는 과정으로 볼 수 있다.

 이번엔 DDPM에서 ELBO을 살펴보자.

 Jensen's Inequality를 사용하였고 식을 더 전개하면

 마지막 식은 markov property로 확률을 대체하고 의미없는 변수들을 다 적분해버리면 나오게 된다. 그럼 이 식은

 이런 세가지 term이 되는데

 먼저 reconsturction term은 VAE와 동일하고

 그 다음 prior matching term은 

 두번째 제약 조건에 의해 encoder는 아래 분포로 고정되고

 세번째 제약 조건에 의해 마지막 잠재변수의 분포는 

 이기 때문에 학습되는 파라미터가 없다. 즉, constant이다.

 마지막 consistency term은 

 디코더의 분포와 인코더의 분포의 차이의 기대값을 모든 항에 대해 계산하는 term으로 의미적으론 reverse process를 forward process에 맞추는 term이다. 그러나 이 term의 Monte Carlo estimate(확률론적 방법을 사용하여 기댓값이나 적분을 계산하는 방식, 주로 random sampling을 사용한다.)는 두 개의 변수를 매 time steps마다 다루기 때문에 높은 variance를 야기한다. 따라서 이를 해결하기 위해 한 step마다 하나의 변수에 대한 기댓값을 구하도록 바꿔어야 한다.

 이는 생각보다 간단하게 해결되는데 markov property로 식을 변형하면 해결된다.

 encoder의 변분 분포를 이렇게 바꿔주면

log내에 곱으로 되어 있는 항들이 cancellation이 일어나게 된다. 

그럼 최종식은

이렇게 되어

 consistency term이 denoising matching term으로 바뀐 것을 알 수 있다.

 Denoising matching term을 좀 더 자세히 살펴보면 왼쪽 식은 encdoer에서 만든 denoising ground-truth signal인데

이렇게 표현된다. 이 수식이 참 만만치 않은데 x_t를 reparameterization으로 구했다 가정하고 접근해보겠다.

 이 수식에서 이상한 부분이라면

 이 부분인데 쉬운 말로 '정규분포는 정규분포를 낳는다.'라는 말에서 유래한 것이다. 자세한 수식은 잡지식에 올려두겠다.

(왜 정규분포는 정규분포를 낳을까?)

2024.05.31 - [다양한 분야의 잡지식] - 말 그대로 다양한 분야의 잡지식

 그럼 이 과정을 확장하여

에 도달하고 추가로 쓰였던 성질의 함수를 전개하면

다시 돌아와서 denoising matching term은

decoder와 ecoder 사이의 차이를 최소화하는 term이다. 그런데 두 정규분포 사이의 KL divergence는 비교적 쉽게 계산되는데

이므로 세타를 최적화 하는 것은 결국 생성 과정의 뮤세타가 인코더의 뮤큐와 같게하는 것이다. 따라서 뮤세타를 뮤큐와 같은 형태로 설계하는 것이 자연스럽고 T시점부터 출발하기 때문에 모르는 x_0를 각 층마다 예측하게 되는 것이다. 이렇게 정한 뮤세타와 뮤큐를 다시 대입하면 

이러한 결론에 도달한다.

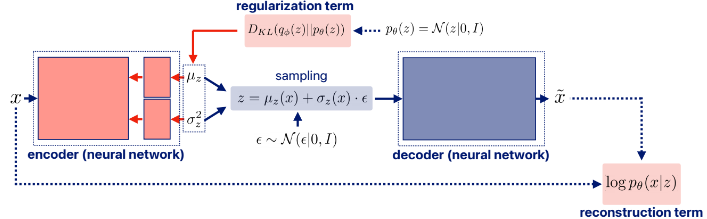
DDPM에서는 다른 추가적인 FC layers와 U-Net architecture를 둬서 t시점의 x_0를 예측한다.

 위 그림에 표현되지는 않았지만 skip connections(고해상도의 이미지를 저해상도에 전달하는 것)가 있고 이 과정은 매 time마다 진행된다.

 그런데 여기서 DDPM을 더 개선한 방식이 있는데

 x_0를 마치 x_t와 노이즈의 결합으로 해석하는 방식이다. 그럼 예측한 뮤세타 역시

이런 꼴로 바뀌게 되고 목적함수는

 noise에 대한 식으로 바뀌게 된다.

이렇게 노이즈를 예측하는 방식이 주로 쓰인다고 하는데 그 이유는 노이즈 예측 방식이 더 안정적이고, 학습 과정에서 더 좋은 성능을 보이는 것으로 나타났기 때문이다.

 추가로 DDPM을 응용하는 것으로 주어진 conditions하에서 generate하는 방식이 있는데 encoder는 fix하고

 이미지를 generate하는 방식에서 조건 이미지를 추가로 넣어 U-Net 구조를 학습시킨다.

 그럼 이렇게 훈련된 모델은 각각 새로운 이미지에 대해 해상도를 복원할 수 있고 색체화가 가능하다.

 마지막으로 여러 generative models를 비교해보면

 Diffusion Models는 아무래도 time의 길이가 길어 fast sampling은 힘들지만 high quality와 diversity한 sample을 만든다는 강점이 있다.

 3. 마무리

 이번 포스트에선 diffusion의 가장 간단한 모델인 DDPM을 알아보았다. 이제 preview 영상으로 가봅시다.

3. Preview 영상

 스터디가기 전에 보기로한 영상에 대해 정리해보겠다.

Diffusion Model 수학이 포함된 tutorial (youtube.com)

 읽어보니까 꽤나 DDPM을 이 post에서 깊게 다루어서 생각보다 흐름을 이해하는데는 어렵지 않았다. Preview 영상이니 자세한 수식보단 큰 흐름과 위에 없는 내용 위주로 요약하겠다.

• Denoising Diffusion Models는 두 과정으로 이루어진다.:
  • Foward diffusion process -> noising
  • Reverse denoising precess -> denoising

• 이렇게 알파 바를 잡았던 것이 특정 시점의 x를 한번에 예측하기 위해서였다.

• intractable은 다루기 어려움을 의미한다.

• ELBO 대신 variational upper boudn로 loss를 정의한다.

• noise만으로도 예측 가

• diffusion은 weighting을 equally하게 적용하지만 advanced weighting도 있다.

• Time representation에 사용되는 것으로 sinusoidal positional embeddings(트랜스포머에서 쓰임)와 random Fourier features가 있다.

• DDPM은 reverse의 시그마 t를 베타 t로 두지만 이 역시 학습가능하다.

• T가 작을수록 high-frequency content = low-level details를 생성한다.

• DDIM: 마르코브 property가 아닌 x_0가 모든 x에 영향을 준다.(Non-Markovian diffusion process)

• Score-based Generative Modeling with Differential Equations

SDE 하에서 score-based model과 diffusion이 사실 같다는 놀라운 사실

 수식이 꽤나 어려워보인다.

• 좀 더 deterministic한 모델

• 특정 조건하에서 생성하는 모델

• 새로운 classifier를 도입하여 구현하는 방식

• 마지막으로 직접 만드신 tree

 Preview 영상이 이해가 하나도 안가서 이번학기에 들은 수업자료를 먼저 되짚어보겠다.

1. MLDL2 수업 - VAE 

0. Intro.

 Data distribution을 알면 p(x)를 기반으로 새로운 samples를 만들거나 새로운 데이터 $\widetilde{x}$가 기존에 관측된 data와 유사한지 판단할 수 있다. 따라서 우리는 model을 통해 data distribution을 approximate하는 것이 목표이고 data distribution을 approximate한다는 것은 observed data x에 대해 likelihood p(x)를 maximize하는 것과 같다.(model에서도 관찰된 데이터가 '관찰'될 확률을 높인다는 것) 

 하지만 우리의 data는 보통 high-dimensional하기 때문에 그 분포는 매우 complex하다. 이를 해결하기 위해 indirect approach인 laten variable methods를 사용한다.

 이 접근방법은 우리의 관측된 x가 관측되지 않는 미지의 변수인 z로부터 생성됬다고 가정하는 것이다. 보통 이 미지의 변수를 latent variable 혹은 hidden variable인데 low-dimensional임이 자연스럽다.(high-dimensional하면 도입할 이유가 없다!) 

 이제 우리는 modeling하려던 p(x) 대신 p(x,z)를 예측하면 되고 이 p(x,z)는 p(z)와 p(x|z) 두개의 곱으로 이루어진다. 즉,

 여기서의 likilihood는 우리가 도입한 변수인 z와 x 사이간의 likelihood이고 p(z)는 우리가 가정한, 추측한 확률이므로 prior probability로 해석한다.

 이렇게 latent variable을 도입한 예시로 gaussian을 활용한 방법이 있다.

 Data distribution이 gaussians의 mixtue N개로 되어있다고 가정하여 data가 그 중 하나로부터 생성되었다고 해석한다.

  이 관점의 특징은 z를 discrete variabe로 본다는 것이다. 따라서 z의 분포는 각 값을 가질 확률로 표현되는 discrete distribution이고 각 data는 자신이 generate된 gaussian의 index인 component index를 갖는다. 

 이 아이디어를 확장한 latent variable model로 non-linear lattent variable model이 있는데 이 모델은 latent variable z가 countinuous variable이고 nomarl prior로 부터 sampling되었다고 가정한다. 즉, 

  그런데 Conditional probability의 mean을 예측하는 f(z)는 신경망 같은 함수인 non-linear function 이기 때문에 위 적분이 불가능하다.(선형이면 가능) 그러니까 지금 생긴 문제를 정리해보면 우리는 p(x)의 likelihood를 maximize해야 하는데 직접 접근하는 것이 어려워 latent variable을 도입했지만 그럼에도 불구하고 closed form이 존재하지 않는 상황인 것이다.

 따라서 이를 해결하기 이해 lower bound를 도입해 proxy objectibve(대리 목적함수)를 사용한다.

1 . ELBO: Evidence Lower Bound

  ELBO에서 evidence는 observed data의 log-likelihood를 의미한다. 즉, ELBO는 위에서 말한 proxu objective인것.

 이제 ELBO를 어떻게 해석할지 알아보기 위해 Jensen's Inequality로 식을 전개해볼 것인데 먼저 Jensen's Inequality는 다음과 같다.

 log function은 concave하기 때문에 평균의 함수값이 함수값의 평균보다 큰 성질을 이용할 것이다. 그럼,

 이렇게 식이 전개되고 

 ELBO는 위와 같이 쓸 수 있다. 여기서 세타는 p를 결정하는 parameters이고 파이는 q를 결정하는 파라미터이다.

2. Variational Inference(VI) 

 그 다음은 ELBO를 최대화 하는 과정을 배울 것인데 처음 배울 때 매우 신기한 아이디어인 VI에 대해 알아보자. ELBO를 이렇게 전개할 수도 있다.

 x와 z의 joint distribution에 z에 대한 posterior를 도입한 것인데(이게 참 웃긴게 우리는 z가 x를 만들었다고 가정했지만 여기서의 확률은 given x, z의 분포에서 얻은 확률이다.)  ELBO가 원래 우리가 구하려던 evidence에 z의 분포와 p(z|x)의 KL-divergene를 뺀 것이라는 것이다. 즉, tight한 바운드는 두 분포 z를 예측한 분포(q), z의 posterior이 같았을 때이다.

 그럼 우리는 ELBO를 어떻게 maximize할까? 우리는 E-M Method(Expectation-Maximization Method, velog에 올라와있는데 추후 가져올 예정..)를 통해 세타와 파이를 번갈아가면서 최적화 해 evidence의 max에 가까워질 수 있다. 즉, 간접적으로 intractable(적분 불가능한) evidence를 optimize하는 것이다.

 위에서 말한 expectation과 maximization 과정은 각각 tight한 bound를 만드는(파이를 update), bound를 개선하는(세타를 update)하는 것인데 그림으로 나타내면 다음과 같다.

 하지만 여기까지 글을 읽을 보면서 이상한 점이 느껴져야 하는데 z의 posterior이 과연 뭐냐는 것이고 계산할 수 있냐는 것이냐이다.

  식을 보면 posterior를 알기 위해선 p(x)를 알아야한다.(p(x)가 어려워서 z도입했더니 p(x)를 계산해야 하는 웃픈 상황) p(x)는 매우 복잡한 분포여서 이 식 역시 계산할 수 없으므로 E-M method를 사용하지 못한다.

 그래서 사용하는 방법이 variational approximation인데 이 방법은 간단한 parametric distribution으로 근사하는 방법으로 z의 posterior를 가우시안 분포로 근사한다.(q를 구하는 parameters인  파이는 variational parameters라 하고 복잡한 함수를 근사하여 추론하는 것을 variational inference라 한다. 그리고 variational parameters는 당연히 x에 딸라 달라지므로 x에 대한 함수로 볼 수 있다.)

 물론 이 발상이 항상 타당한 것은 아니다. 아래 그림에서는 꽤나 괜찮은 근사를 하지만

 이 그림에선 매우 poor하다.

 다시 그동안 했던 것들을 되돌아보면

 Evidence를 maximize하려던 목표는 ELBO을 maximize하는 것으로 바뀌었고 이는 q(z)와 p(z|x)의 차이를 최소화하는 과정이 필요했으나 불가능하여 variational approximation을 사용한다. 마치

를 하는 것과 같아진 것.

3. Variational Auto-Encoder(VAE)

 이번엔 VI를 응용한 신경망인 VAE에 대해 알아보자. VAE는 x를 latent variable z로 encoding하고 이를 다시 decoding하여 x와 유사한 x틸다를 생성하는 것이다. z에 대한 posterior이 아닌 prior를 도입해보자.

 여기서 왼쪽 term은 reconstruction term이라 하는데

 근사된 z(q(z)의 확률 분포를 갖는 z)에서 x가 잘 re-generate되는지 확인하는 term이다. 값은 당연히 크면 클수록 잘 근사한 것이다.

 오른쪽 term은 regularization term인데 

 근사한 z의 분포가 실제 z의 분포(prior)과 유사해는지 확인하는 term이다. 값이 크면 차이가 큼을 의미하므로 -가 붙는다.

 일반적으로 VAE에서 z의 prior는 N(0,1)로 가정한다.

  Regularization term을 보면 (생략되었지만 두 분포 모두 given x에서 얻어졌다.) 따라서 variational parameters 역시 VI와 마찬가지로 x에 대한 함수이다. VI에선 언급하지 않았지만 이 부분이 문제가 되는데 그럼 모든 x에 대해서 파이를 계산해야 하는 문제가 생겨 scalable하지 않다.(scalable하다는 것은 많은 양의 x에서도 합리적인 계산이 가능해 확정가능함을 의미한다.) 

 따라서 VAE에서 도입한 것이 encoder architecture인데 이 구조로 amortized inference가 가능하다.

 뭔 소리냐? x를 입력하면 뮤와 시그마를 출력하는 신경망을 만드는 것. 이 신경망 하나를 학습시키면 각 파라미터를 모두 학습시키는 것보다 훨씬 간단해진다.(amortized는 '공통으로, 한꺼번에'를 의미한다.) 

 이렇게 만든 q(z|x)에서 z를 sampling하고 decoder를 통해 x 틸다를 만들어 낸다.

 그럼 실제로 reconstruction term을 어떻게 계산하는지 알아보자.

 VAE 역시 신경망이다 보니 differentiable이 필수이다. 하지만 sampling process는 일반적으로 non-differentiable이다. 따라서 우린 reparameterization trick을 통해 이 과정을 미분가능하게 할 것인데 z를

로 sampling하고 gradient를 계산하는 것이다. z의 prior이 N(0,1)으로 unbiased하고 minibatch size가 클 때 이렇게 one sample로 gradient를 계산하여도 동일한 효과를 내는 것은 수학적으로 밝혀져있다.(이부분은... 납득!) 

 이후 decoder 과정에서 x 틸다를 N(x|x*, I)에서 sampling하는데(시그마를 1로 가정) 이 때

가 성립한다.(x_{rec} = x 틸다)

 왜냐하면 가우시안 분포가

이렇게 생겼는데 log를 씌우면

 이고 앞 항은 constant여서

이다. 즉, 의미를 분석하면 reconstruction term은 x와 x 틸다 사이의 유클리드 거리의 제곱이 최소화되도록 학습하는 것이다.

 이번엔 regularization term을 살펴보자.

 p(z)는 일반적으로 N(0,1)로 가정하고 q(z)는 z의 posterior 인데 이 역시 Gaussian distribution이므로 위 식은 closed form이 존재해 생각보다 쉽게 계산된다.

 즉, sampling을 포함한 전체 process를 보면

가 된다. 이제 각 term이 어느 층과 연결되는지까지 표현하면

 이렇게 되고 역전파를 나타내면

 와

이다. 결론적으로 우리는 latent variable z를 통해 새로운 것을 'generation' 할 수 있게 되었다.

+

이 주석을 봤을 때 의문이 들어야 하는 것이 'x 틸다를 sampling한다.'는 표현이다. 그럼,

이 backporpagation에서 x 틸다는 sampling process를 거치기 때문에 미분이 가능한지 의구심을 들게 만든다.

결론부터 말하면 둘다 맞다.

 우선 미분이 가능한 이유는 deocder는 주어진 z에 대해 하나의 결정적인 출력을 만든다. 즉, 주어진 z에 대해 항상 동일한 x 틸다를 생성하는 것이다.(x 틸다 = g(z)) 그럼, sampling 했다고 표현할 수 있는지 생각이 들 수 있는데 x가 잠재 변수 z로부터 생성될 때 가우시안 분포로부터 생성된다고 가정했기 때문에 하나의 sample을 추출한 것으로 해석할 수 있다. 당연히 정규 분포에서 가장 가능성이 높은 평균을 sample하는 것이 자연스럽기 때문에 이 x틸다는 z로부터 출력한 p(x|z_ 분포의 평균이고 이를 통해 reconstruction term을 계산한다. 

 정리하면 z를 통해 x가 바로 결정되고 x는 p(x|z)에서 하나 sampling 된 것으로 볼 수 있다.

4. Hierachical Variational Auto-Encoder(HVAE)

 VAE에서 latent variable이 여러 개로 확장되고 각각이 depencency가 존재하는 모델이 HVAE이다. 이는 diffusion의 기반이 되니 다음 포스트에서 또 언급하겠다.

 5. Recurrent VAE

 VAE를 확장한 또다른 구조로 recurrent VAE가 있다. Hidden variables 사이에 recurrence가 존재하는 것이 특징이다.

6. Problems with VAE

1. inefficient to evaluate / measure the likelihood of observed data

: 애초에 위 과정이 모두 이루어진 것이  p(x|z)p(z)dz가 적분이 되지 않아 이런 먼길을 돌아온 것이다. 적분을 학술이는 방법이 있긴 하지만(MCMC(Markov Chain Monte Carlo) 방법은 복잡한 확률 분포에서 샘플링하여 적분 문제를 해결하는 강력한 수치적 방법) 계산 과정이 매우 많아 비효율적이다.

2. not perfect samples from the distribution

: 1번 때문에 간단한 함수로 근사하는 variational inference를 하지만 '간단한' 함수이기 대문에 생성하는데 완벽하지 않다. 즉 normal distribution으로 복잡한 분포는 근사하기에는 충분하지 않다. 실제로 생성해보면 over smoothing한 x 틸다가 아래처럼 생긴다.

3. posterior collapse with strong decoder

: 만약 decoder가 너무 강하면(capacity가 크다면) 잠재변수 z를 무시하고 그냥 x로부터 x틸다를 구성해버린다. Encoder를 사용하지 않지만 마치 학습되는 것처럼 보이기 대문에 모델의 표현력이 개선되지 않는다.

7. 마무리

 이렇게 저번 기말 범위 중 하나였던 VAE에 대한 내용을 마치고 다음 포스트는 HVAE에 제약을 더한 diffusion에 대해 올려보겠다. (지금부터 해야 되긴해..)