다양하지만 얕지 않게

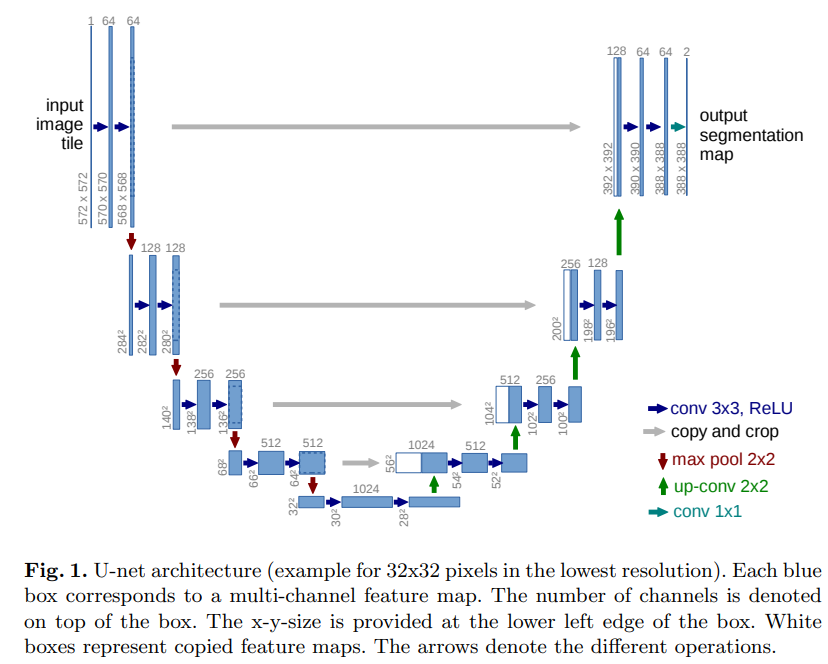
 이번엔 기말고사 전에 리뷰했던 U-Net을 구현해보는 시간을 가져볼 것이다. 리뷰했을 때에 언급했지만 U-Net은 biomedical dataset에 특화된 모델이어서 sub task 역시 bio에 관련된 것으로 가져왔다.

1. Task와 Dataset 소개

 오늘의 dataset은 아래에 올라와있다.

https://www.kaggle.com/datasets/andrewmvd/cancer-inst-segmentation-and-classification 

 전체 데이터셋은 크게 3개로 나눠있는데 하나의 part만 가져와도 256*256의 이미지가 2656개가 있어서 충분하다고 판단해(사실 충분한단 것은 gpu memory의 한계를 의미하는 것과 같다.) part 1만 사용하였다.
  Author Notes의 README를 읽어보면 19개의 tissue types의 데이터로 이루어져있으며 각각은 0: Neoplastic cells, 1: Inflammatory, 2: Connective/Soft tissue cells, 3: Dead Cells, 4: Epithelial, 6: Background 이렇게 마스킹 되어있다.
 용어를 하나하나 살펴보면
 

Neoplastic cells : 종양을 형성하는 세포
Inflammatory : 염증성
Connective/Soft tissue cells: 결합조직 및 연조직으로 신체의 구조와 지지 기능을 담당하는 세포들
Dead Cells: 죽은 세포, 더 이상 기능하지 않는 세포
Epithelial: 상피 세포, 신체의 표면과 내부 장기를 덮고 있는 세포
 

인데 오랜만에 생물 공부를 하는 느낌이다.
 그리고 추가적으로 데이터 형식을 살펴보면 특이하게 images와 masks가 images.npy, masks.npy로 되어 있다는 것이다. 
(npy 파일은 NumPy 라이브러리에서 사용하는 파일 형식으로, 다차원 배열 데이터를 효울적으로 저장하고 로드하는데 사용된다.)

import numpy as np

images = np.load(r'C:\Users\james\Desktop\U-net\Part 1\Part 1\Images\images.npy', mmap_mode='r')
images = images.astype('int32')

masks = np.load(r'C:\Users\james\Desktop\U-net\Part 1\Part 1\Masks\masks.npy', mmap_mode='r')
masks = masks.astype('int32')

print(images.shape)
print(masks.shape)

 (코드의 mmap_mode 매개변수는 매모리 맵핑을 사용하여 대용량 배열 데이터를 디스크에서 직접 읽는 방식을 지정하는데 사용한다. 이 값을 기본값으로하게 되면 매모리 맵핑을 사용하지 않아 파일 전체가 메모리에 로드되는데 파일 양이 커서 local의 경우 과부화가 걸린다. 따라서 읽기 전용 모드로 파일을 메모리에 매핑하여 데이터의 일부만 로드하고 필요한 부분만 읽게 하였다. 즉, 메모리 사용량을 줄이고 입출력 성능을 향상시키기 위해 하는 것!)

(2656, 256, 256, 3)
(2656, 256, 256, 6)

 출력해보면 masks의 채널이 왜 6인지는 위에 데이터셋을 보면 알 수 있을 것이다. 일전의 FCN에서 했던 cloth segmentation의 경우 semantic segmentation이기 때문에 2차원 mask에서 각 pixel의 값에 class의 number를 매핑하면 충분하였다. 하지만 이번 task는 instance segmentation을 해야하기 때문에 3차원 mask에 각 채널이 하나의 class를 의미하고 각 class에 해당하는 instance를 숫자로 매핑하게 되었다.
 Semantic segmentation과 instance segmentation이 무엇이지 까먹었다면 이 곳으로

2024.04.26 - [DL/Image Segmentation] - [Paper Review] Fully Convolutional Netowrks for Semantic Segmentation

 그럼 task와 데이터 소개를 마쳤으니 본격적인 구현 단계로 넘어가 보겠다.

2. Dataset  정의 및 Dataset 로딩

import torch
from torch.utils.data import Dataset, DataLoader
from PIL import Image

class NumpySegDataset(Dataset):
    def __init__(self, images_path, masks_path, transform=None, target_transform=None):
        self.images = np.load(images_path, mmap_mode='r')
        self.masks = np.load(masks_path, mmap_mode='r')
        self.transform = transform
        self.target_transform = target_transform

    def __len__(self):
        return len(self.images)

    def __getitem__(self, idx):
        image = self.images[idx]
        mask = self.masks[idx]

        if self.transform:
            image = self.transform(image)

        if self.target_transform:
            mask = self.target_transform(mask)

        # image는 정규화하면 소수로 변하니까 float, mask는 정규화 안하니까 int
        image = torch.tensor(image, dtype=torch.float32).permute(2,0,1)
        mask = torch.tensor(mask, dtype=torch.int64).permute(2,0,1)

        return image, mask

 항상 해왔듯이 Dataset class인 NumpySegDataset class를 정의하고 __init__,. __len__함수와 __getitem__ 함수를 정의하였다. 다만 저번 미니 프로젝트와는 다른 점은 __init__ 함수를 만들 때 numpy 배열이기 때문에 np.load와 mmap_mode = 'r'이라는 점이다.

images_path=r'C:\Users\james\Desktop\U-net\Part 1\Part 1\Images\images.npy'
masks_path=r'C:\Users\james\Desktop\U-net\Part 1\Part 1\Masks\masks.npy'

dataset = NumpySegDataset(images_path, masks_path)

 이렇게 dataset을 정의해주었고

total_len = len(dataset)
train_len = int(total_len * 0.8)
val_len = total_len - train_len

train_dataset, val_dataset = torch.utils.data.random_split(dataset, [train_len, val_len])
train_loader = DataLoader(train_dataset, batch_size=4, shuffle=True)
val_loader = DataLoader(val_dataset, batch_size=4, shuffle=True)

 dataset을 로딩해줄 때 8:2의 비율로 train과 validation을 구분하였다.
 (batch size가 4로 매우 작은 편인데 batch size를 좀만 늘려도 OOM(Out of Memory) 문제가 발생하여서 batch size와 epoch를 모두 줄이게 되었다.)

 3. 모델 architecture 정의

 먼저 참고한 사이트는 다음과 같다.
https://github.com/meetps/pytorch-semseg/blob/master/ptsemseg/models/unet.py

https://www.kaggle.com/code/pedroamavizca/working-with-u-net

 이번에 U-Net class를 만들 때 구현하고자 하는 내용은 다음과 같다.

1. U-Net 구조
2. pixel-wise weight와 cross entropy를 결합한 custom_loss
3. mirroring extrapolation

 그래서 먼저 U-Net 구조를 만들면

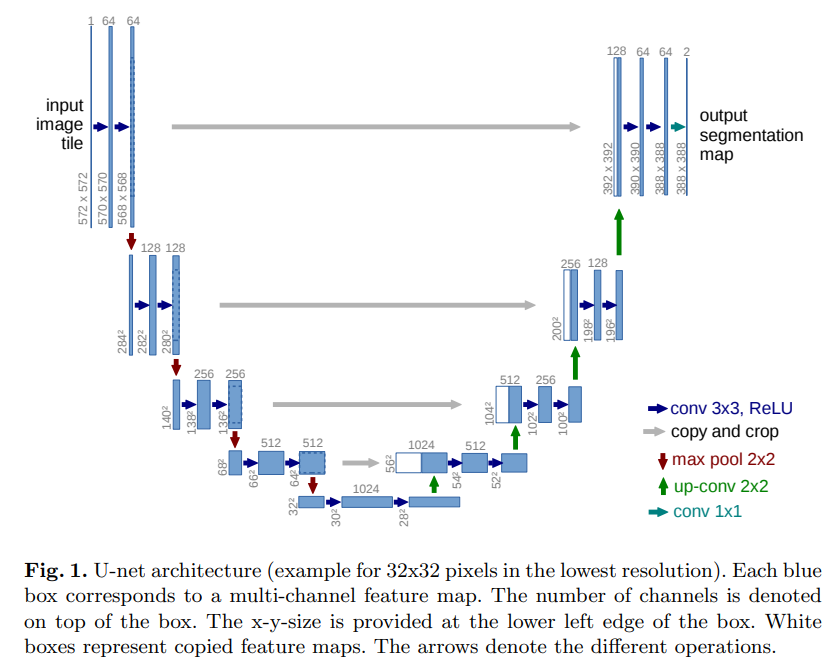
이 구조를 만들어야 하기 때문에 반복적으로 있는 conv 3*3, ReLU(위 그림에서 파란색 2개)를 하나의 class로 정의해보겠다.

class UNetConv2(nn.Module):
    def __init__(self, in_channels, out_channels):
        super(UNetConv2, self).__init__()
        # (입력크기+2*패딩-커널크기)/스트라이드+1
        self.conv1 = nn.Sequential(
            nn.Conv2d(in_channels, out_channels, kernel_size=3, stride=1, padding=0),
            nn.BatchNorm2d(out_channels),
            nn.ReLU()
        )
        self.conv2 = nn.Sequential(
            nn.Conv2d(out_channels, out_channels, kernel_size=3, stride=1, padding=0),
            nn.BatchNorm2d(out_channels),
            nn.ReLU()
        )

    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2(x)
        return x

 그 다음 이를 활용하는 전체 U-Net class를 정의하면

class UNet(nn.Module):
    def __init__(self, num_classes=6, in_channel=3):
        # 부모 클래스 초기화되어 자식 클래스에서도 사용 가능
        super(UNet, self).__init__()
        self.conv_1 = UNetConv2(in_channel, 64)
        self.conv_2 = UNetConv2(64, 128)
        self.conv_3 = UNetConv2(128, 256)
        self.conv_4 = UNetConv2(256, 512)

        self.mid_conv = UNetConv2(512, 1024)

        self.conv_5 = UNetConv2(1024, 512)
        self.conv_6 = UNetConv2(512, 256)
        self.conv_7 = UNetConv2(256, 128)
        self.conv_8 = UNetConv2(128, 64)

        self.down = nn.MaxPool2d(kernel_size=2, stride=2)
        self.up_1 = nn.ConvTranspose2d(1024, 512, kernel_size=2, stride=2)
        self.up_2 = nn.ConvTranspose2d(512, 256, kernel_size=2, stride=2)
        self.up_3 = nn.ConvTranspose2d(256, 128, kernel_size=2, stride=2)
        self.up_4 = nn.ConvTranspose2d(128, 64, kernel_size=2, stride=2)

        self.end = nn.Conv2d(64, num_classes, kernel_size=1, stride=1)

    def forward(self, x):
        padded_x = F.pad(x, (92, 92, 92, 92), mode='reflect')
        conv_1 = self.conv_1(padded_x) # output: 252*252
        if conv_1.size()[2] % 2 != 0:
            conv_1 = F.pad(conv_1, (0, 1, 0, 1))
        pool1 = self.down(conv_1) # output: 126*126

        conv_2 = self.conv_2(pool1) # output: 122*122
        if conv_2.size()[2] % 2 != 0:
            conv_2 = F.pad(conv_2, (0, 1, 0, 1))
        pool2 = self.down(conv_2) # output: 61*61

        conv_3 = self.conv_3(pool2) # output: 57*57
        if conv_3.size()[2] % 2 != 0:
            conv_3 = F.pad(conv_3, (0, 1, 0, 1))
        pool3 = self.down(conv_3) # output: 29*29

        conv_4 = self.conv_4(pool3) # output: 25*25
        if conv_4.size()[2] % 2 != 0:
            conv_4 = F.pad(conv_4, (0, 1, 0, 1))
        pool4 = self.down(conv_4) # output: 13*13

        mid_conv = self.mid_conv(pool4) # output: 9*9

        up_1 = self.up_1(mid_conv)
        scale_idx_1 = (conv_4.shape[2] - up_1.shape[2]) // 2
        cropped_conv_4 = conv_4[:, :, scale_idx_1:-scale_idx_1, scale_idx_1:-scale_idx_1]
        up_1 = torch.cat([up_1, cropped_conv_4], dim=1)
        conv_5 = self.conv_5(up_1)

        up_2 = self.up_2(conv_5)
        scale_idx_2 = (conv_3.shape[2] - up_2.shape[2]) // 2
        cropped_conv_3 = conv_3[:, :, scale_idx_2:-scale_idx_2, scale_idx_2:-scale_idx_2]
        up_2 = torch.cat([up_2, cropped_conv_3], dim=1)
        conv_6 = self.conv_6(up_2)

        up_3 = self.up_3(conv_6)
        scale_idx_3 = (conv_2.shape[2] - up_3.shape[2]) // 2
        cropped_conv_2 = conv_2[:, :, scale_idx_3:-scale_idx_3, scale_idx_3:-scale_idx_3]
        up_3 = torch.cat([up_3, cropped_conv_2], dim=1)
        conv_7 = self.conv_7(up_3)

        up_4 = self.up_4(conv_7)
        scale_idx_4 = (conv_1.shape[2] - up_4.shape[2]) // 2
        cropped_conv_1 = conv_1[:, :, scale_idx_4:-scale_idx_4, scale_idx_4:-scale_idx_4]
        up_4 = torch.cat([up_4, cropped_conv_1], dim=1)
        conv_8 = self.conv_8(up_4)

        end = self.end(conv_8)
        scale_idx_5 = (end.shape[2]-x.shape[2]) // 2
        end = end[:, :, scale_idx_5:-scale_idx_5, scale_idx_5:-scale_idx_5]

        return end

 다음과 같은데 최대한 논문에서 말하는 구조를 따라하기 위해 padding을 0으로 하고 croppping하는 과정을 넣었는데 참고한 사이트에선 구현을 용이하기 위해 padding을 사용하였다. 그리고 논문에서 segmentation이 용이하게 되기 위해서는 max pooling을 하는 input의 size가 짝수여야 했는데 이미 이미지의 크기가 256*256으로 제한되어 있어서 이를 늘리거나 줄이지는 않고 홀수 일때만 padding을 추가하는 방식으로 구현하였다.
 torch.summary를 사용해 출력해보면 다음과 같다.

torch.Size([500, 256, 256])
torch.Size([500, 256, 256])
torch.Size([500, 256, 256])
torch.Size([500, 256, 256])
torch.Size([500, 256, 256])
torch.Size([156, 256, 256])
torch.Size([2656, 256, 256])

(2656, 256, 256, 3)
(2656, 256, 256, 6)
torch.Size([16, 3, 256, 256])
----------------------------------------------------------------
        Layer (type)               Output Shape         Param #
================================================================
            Conv2d-1         [-1, 64, 438, 438]           1,792
       BatchNorm2d-2         [-1, 64, 438, 438]             128
              ReLU-3         [-1, 64, 438, 438]               0
            Conv2d-4         [-1, 64, 436, 436]          36,928
       BatchNorm2d-5         [-1, 64, 436, 436]             128
              ReLU-6         [-1, 64, 436, 436]               0
         UNetConv2-7         [-1, 64, 436, 436]               0
         MaxPool2d-8         [-1, 64, 218, 218]               0
            Conv2d-9        [-1, 128, 216, 216]          73,856
      BatchNorm2d-10        [-1, 128, 216, 216]             256
             ReLU-11        [-1, 128, 216, 216]               0
           Conv2d-12        [-1, 128, 214, 214]         147,584
      BatchNorm2d-13        [-1, 128, 214, 214]             256
             ReLU-14        [-1, 128, 214, 214]               0
        UNetConv2-15        [-1, 128, 214, 214]               0
        MaxPool2d-16        [-1, 128, 107, 107]               0
           Conv2d-17        [-1, 256, 105, 105]         295,168
      BatchNorm2d-18        [-1, 256, 105, 105]             512
             ReLU-19        [-1, 256, 105, 105]               0
           Conv2d-20        [-1, 256, 103, 103]         590,080
      BatchNorm2d-21        [-1, 256, 103, 103]             512
             ReLU-22        [-1, 256, 103, 103]               0
        UNetConv2-23        [-1, 256, 103, 103]               0
        MaxPool2d-24          [-1, 256, 52, 52]               0
           Conv2d-25          [-1, 512, 50, 50]       1,180,160
      BatchNorm2d-26          [-1, 512, 50, 50]           1,024
             ReLU-27          [-1, 512, 50, 50]               0
           Conv2d-28          [-1, 512, 48, 48]       2,359,808
      BatchNorm2d-29          [-1, 512, 48, 48]           1,024
             ReLU-30          [-1, 512, 48, 48]               0
        UNetConv2-31          [-1, 512, 48, 48]               0
        MaxPool2d-32          [-1, 512, 24, 24]               0
           Conv2d-33         [-1, 1024, 22, 22]       4,719,616
      BatchNorm2d-34         [-1, 1024, 22, 22]           2,048
             ReLU-35         [-1, 1024, 22, 22]               0
           Conv2d-36         [-1, 1024, 20, 20]       9,438,208
      BatchNorm2d-37         [-1, 1024, 20, 20]           2,048
             ReLU-38         [-1, 1024, 20, 20]               0
        UNetConv2-39         [-1, 1024, 20, 20]               0
  ConvTranspose2d-40          [-1, 512, 40, 40]       2,097,664
           Conv2d-41          [-1, 512, 38, 38]       4,719,104
      BatchNorm2d-42          [-1, 512, 38, 38]           1,024
             ReLU-43          [-1, 512, 38, 38]               0
           Conv2d-44          [-1, 512, 36, 36]       2,359,808
      BatchNorm2d-45          [-1, 512, 36, 36]           1,024
             ReLU-46          [-1, 512, 36, 36]               0
        UNetConv2-47          [-1, 512, 36, 36]               0
  ConvTranspose2d-48          [-1, 256, 72, 72]         524,544
           Conv2d-49          [-1, 256, 70, 70]       1,179,904
      BatchNorm2d-50          [-1, 256, 70, 70]             512
             ReLU-51          [-1, 256, 70, 70]               0
           Conv2d-52          [-1, 256, 68, 68]         590,080
      BatchNorm2d-53          [-1, 256, 68, 68]             512
             ReLU-54          [-1, 256, 68, 68]               0
        UNetConv2-55          [-1, 256, 68, 68]               0
  ConvTranspose2d-56        [-1, 128, 136, 136]         131,200
           Conv2d-57        [-1, 128, 134, 134]         295,040
      BatchNorm2d-58        [-1, 128, 134, 134]             256
             ReLU-59        [-1, 128, 134, 134]               0
           Conv2d-60        [-1, 128, 132, 132]         147,584
      BatchNorm2d-61        [-1, 128, 132, 132]             256
             ReLU-62        [-1, 128, 132, 132]               0
        UNetConv2-63        [-1, 128, 132, 132]               0
  ConvTranspose2d-64         [-1, 64, 264, 264]          32,832
           Conv2d-65         [-1, 64, 262, 262]          73,792
      BatchNorm2d-66         [-1, 64, 262, 262]             128
             ReLU-67         [-1, 64, 262, 262]               0
           Conv2d-68         [-1, 64, 260, 260]          36,928
      BatchNorm2d-69         [-1, 64, 260, 260]             128
             ReLU-70         [-1, 64, 260, 260]               0
        UNetConv2-71         [-1, 64, 260, 260]               0
           Conv2d-72          [-1, 6, 260, 260]             390
================================================================
Total params: 31,043,846
Trainable params: 31,043,846
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.75
Forward/backward pass size (MB): 1773.24
Params size (MB): 118.42
Estimated Total Size (MB): 1892.42
----------------------------------------------------------------

4. 손실함수와 optimizer 정의

 우선 model과 optimizer는 쉽게 정의했는데

model = UNet().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

 일반적인 loss fucntion을 사용하는 것이 아닌 각 pixel에 weight를 부여하고 softmax함수와 cross entropy loss를 결합한 loss(논문에 잘 소개되어있다.)를 사용해보기 위해 함수들을 정의해보았다.

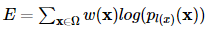
def custom_loss(outputs, labels, weights):
    # softmax 계산
    softmax_outputs = F.softmax(outputs, dim=1)

    # CPU로 이동
    labels = labels.cpu()
    weights = weights.cpu()
    softmax_outputs = softmax_outputs.cpu()

    # 0이 아닌 위치를 찾기 위한 마스크 생성
    non_zero_mask = labels != 0

    # 마스크를 사용하여 필요한 값 선택 및 계산
    selected_weights = weights.unsqueeze(1).expand_as(labels)[non_zero_mask]
    selected_softmax_outputs = softmax_outputs[non_zero_mask]

    # 손실 계산
    running_loss = (-1) * selected_weights * torch.log(selected_softmax_outputs)
    running_loss = running_loss.sum()

    running_loss /= labels.shape[0] * labels.shape[2] * labels.shape[3]

    return running_loss.to(outputs.device)

 먼저 outputs에서 softmax를 적용하고(채널이 class별 출력을 위하니 dim=1로 softmax를 계산한다.) labels에서 0이 아닌 위치를 나타내는 non_zero_mask를 정의하였다. weights의 차원은 (batch_size, height, width)이고 non_zero_mask의 차원은 (batch_size, num_classes, height, width)에서 selected_weights를 구하기 위해선 weights에서 두번째 차원을 추가하고 labels의 num_classes만큼 복사한다음 선택을 한다. 그렇게 계산한 selected_weights의 차원은 non_zero의 갯수가 N이라 하면 (N,)이다. 그리고 필는 loss function을 최소화하기 위해 -1을 붙였고 pixel-wise loss때문에 평균을 내기 위해 batch_size와 height, width로 나누어줬다. 
 그럼 weight는 어떻게 계산할까? 논문에서는

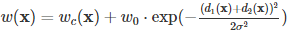
 이렇게 class의 frequency를 반영한 1차 weight에 세포와의 거리를 반영하는 추가적인 weight로 계산하였는데 구현이 엄청 어려운 것이지만 시간이 매우 오래 걸릴 것이라 판단하여 비슷한 아이디어로 정의하였다.

import torch

def find_others(labels, i, j, k, b, d):
    left = max(i - d, 0)
    right = min(i + d, 255)  # 256이 아니라 255까지
    up = max(j - d, 0)
    down = min(j + d, 255)  # 256이 아니라 255까지
    instance = labels[b, k, i, j]

    region = labels[b, k, left:right+1, up:down+1]
    other_classes = (region == 0).sum().item()
    other_instances = ((region != 0) & (region != instance)).sum().item()

    return other_classes, other_instances

def calculate_weights(masks):
    device = masks.device
    batch_size, num_classes, height, width = masks.shape
    weights = torch.zeros((batch_size, height, width), device=device)
    non_zero_counts = (masks != 0).sum(dim=(2, 3))

    for b in range(batch_size):
        non_zero_ratio = non_zero_counts[b].float() / non_zero_counts[b].sum(dim=0, keepdim=True).float()
        exp_non_zero_ratio = torch.exp(-non_zero_ratio)
        
        for k in range(num_classes):
            mask_k = masks[b, k]
            non_zero_mask = mask_k != 0
            weights[b][non_zero_mask] = exp_non_zero_ratio[k]

            for i in range(2, height, 5):
                for j in range(2, width, 5):
                    if non_zero_mask[i, j]:
                        other_classes, other_instances = find_others(masks, i, j, k, b, 2)
                        weights[b, i-2:i+3, j-2:j+3] *= (1.02)**other_classes
                        weights[b, i-2:i+3, j-2:j+3] *= (1.05)**other_instances

    return weights

 기본적인 아이디어는 먼저 class의 frequency의 비율에 exp(-x)를 적용하고 해당 pixel을 가운데로 하는 25개의 pixel에 같은 class지만 다른 instance인 pixel의 개수(a)와 다른 class인 pxiel의 개수(b)에 따라 가중치를 각각 1.05**(a), 1.02**(b) 배 해주는 방식이다. 총 2656개의 데이터의 256*256 pixels는 1억개가 넘어서(174,063,616) 다섯 pixels씩 넘어가면서 계산하도록 설계하였다. 
 matplotlib의 pyplot을 사용하여 하나의 weight를 시각해보면 다음과 같다.

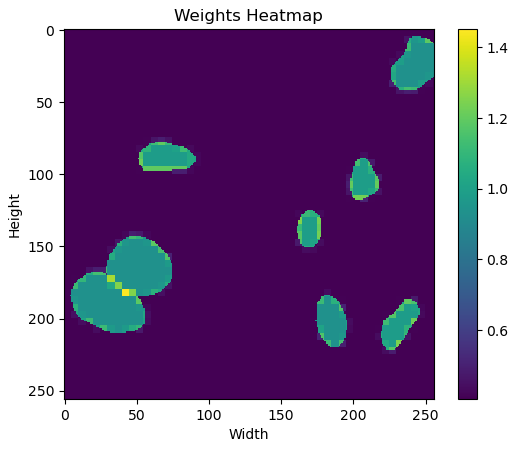
 경계에서, 특히 다른 instance의 경계에서 가장 높은 weight를 갖도록 설계된 것을 알 수있다.

5. Train & Validation

num_epochs = 50  # Number of epochs
batch_size = 4
val_idx_start = len(train_loader.dataset)

for epoch in range(num_epochs):
    print(f'Epoch {epoch+1}/{num_epochs}')

    # Each epoch has a training and validation phase
    for phase in ['train', 'val']:
        if phase == 'train':
            model.train()  # Set model to training mode
            dataloader = train_loader
        else:
            model.eval()   # Set model to evaluate mode
            dataloader = val_loader

        running_loss = 0.0

        # Iterate over data with tqdm for the progress bar
        progress_bar = tqdm(enumerate(dataloader), total=len(dataloader), desc=f"{phase.capitalize()} Phase")
        for batch_idx, (inputs, labels) in progress_bar:
            inputs, labels = inputs.to(device), labels.to(device)

            # Zero the parameter gradients
            optimizer.zero_grad()

            # Forward
            with torch.set_grad_enabled(phase == 'train'):
                outputs = model(inputs)

                if phase == 'train':
                    batch_weights = weights[batch_idx * batch_size : (batch_idx + 1) * batch_size]
                else:
                    batch_weights = weights[val_idx_start + batch_idx * batch_size : val_idx_start + (batch_idx + 1) * batch_size]

                loss = custom_loss(outputs, labels, batch_weights)

                if phase == 'train':
                    loss.backward()
                    optimizer.step()

            # Statistics
            running_loss += loss.item() * inputs.size(0)
            epoch_loss = running_loss / len(dataloader.dataset)

            # Update the progress bar with the current loss value
            progress_bar.set_postfix({'loss': f'{loss.item():.4f}'})

        if phase == 'val':
            print(f'{phase.capitalize()} Loss: {epoch_loss:.4f}')
        print()

 GPU 메모리와 사용량의 한계로 epoch를 50으로 설정하였고 위에서 계산한 weight를 batch에 맞게 가져오도록 설계하였다. 훈련은 총 3시간 정도 걸렸다.

 결과를 시각화해보면

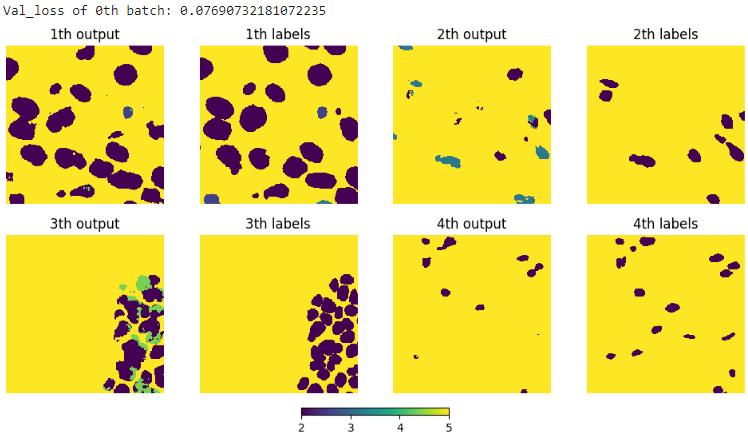
 이렇게 생각보다 output이 labels를 잘 분류하는 것을 알 수 있다. 그런데 필자의 최종 목표는 instance segmentation이기 때문에 watershed 알고리즘을 적용하였다. 아래 그림은 바로 위 그림의 첫번째 output에 적용한 결과인데

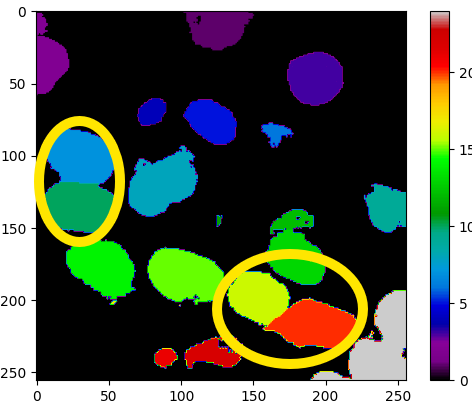
  노란색 타원으로 표시한 부분처럼 touching instances들도 구분한 것을 알 수 있다.
+ watershed 알고리즘
 객체를 분할하는데 사용되는 기법으로 지형학적 모델을 사용하여 이미지의 픽셀을 분할하는기 때문에 outputs의 각 클래스별 출력이 높이로 간주된다. 이 알고리즘은 물이 채워질 때 계곡을 따라 경계가 형성된다는 개념에서 유래됐다. 알고리즘의 단계로는 
1. 전처리 - threshold 보다 낮은 값들은 제거한다.
2. 거리 변환 -  객체 내부의 각 픽셀이 가장 가까운 배경 픽셀로부터 얼마나 떨어져 있는지 계산한다. 여기서 거리는 Manhattan distance를 의미한다. 
3. 마커 생성 - 지역 극대값을 찾아 마커로 설정한다. 마커는 객체의 중심을 나타낸다.
4. watershed 변환 - 마커에서 시작하여 물을 채워 나가, 서로 다른 마커에서 채워진 물이 만나는 지점에서 경계가 형성된다.
 가 있고 그 결과 위 그림처럼 instance segmentation이 수행된다.

 6. 마무리

 위 전체 코드를 구현한 것은 깃허브에 올려두었다.
https://github.com/ParkSeokwoo/U-Net-cancer-instance-segmentation-

 
 Watershed 알고리즘을 진작에 알았다면 loss를 설계하는 과정이 더 논문에 가까워졌을 것 같지만 이 정도만으로 만족하고 넘어가려한다. 그리고 이건 위 모델하고는 상관없는데 생각보다 kaggle notebook이 괜찮은거 같다. Colab pro를 결제해도 다 쓰는데 1주일 밖에 걸리지 않는데 kaggle notebook은 전화번호가 있는데로 쓸 수 있고 1주일마다 다시 30시간을 사용할 수 있기 때문에 앞으로 대부분의 작업을 kaggle에서 사용할 것 같다. 다음 포스트는 동아리 사람들과 diffusion 모델 스터디를 하게 되어서 스터디 준비용 포스트를 올릴 것 같다. 바이~

 이번 포스트는 U-Net을 소개하는 논문을 리뷰해보겠다. 논문은 다음 사이트에 올라와있다.

 https://arxiv.org/abs/1505.04597

 이번 역시 동아리에서 발표했던 주제라 그 때 사용한 피피티를 첨부하겠다.

Abstract

< 내용 >

 Deep nets가 성공적으로 훈련되기 위해서는 많은 annotated training samples가 필요하다고 알려져있다. 우리는 이 논무네서 이용가능한 annotated samples를 더 효율적으로 사용하기 위해 data augmentation을 활용하는 훈련 전략과 network를 소개하려 한다. 그 구조는 context를 캡처하는 contracting path와 정밀한 localization을 가능하게 하는 대칭적인 expanding path로 이루어져있다. 우리는 이 network가 end-to-end 방식으로 학습 가능한데 매우 작은 이미지더라도 기존의 방법인 sliding-window 방식을 능가하는 것을 보일 것이다.(데이터는 ISBI challenge for segmentation of neural structures in electron microscopic stacks) 같은 네트워크를 transmitted light microscopy images에도 훈련하여 ISBI cell tracking challenge 2015에서 가장 좋은 성능을 보였다. 게다가 이 네트워크는 바르다. 512*512 images를 GPU를 사용하여 inference하는데 일 초 이내의 시간이 걸린다.   

< comment >

 저자들이 소개하는 U-net은 기본적으로 FCN의 구조를 따르지만 몇가지 차이점이 존재한다. 대표적인 예시가 contracting path와 expanding path가 symmetric하다는 점인데 뒤에서 자세히 소개하도록 하고 U-Net에서 또 주목할만한 부분은 적은 이미지로도 높은 성능을 달성하기 위해 data augmentation을 사용했다는 점이다. 이는 biomedical image dataset의 특성과 관련되는데 이 dataset은 이미지의 크기가 다양하면서 대부분 크고 개수가 적다는 특징이 있다. 이를 보안하기 위해 U-Net이 어떻게 설계되었는지 차차 알아가보자.

1. Introduction

< 내용 >

 지난 2년동안 deep convolutional networks는 많은 visual recogniton tasks에서 sota를 달성했다. 이러한 성공이 오랜시간 지속되었지만 그들의 성공이 제한되었던 것은 이용가능한 training set의 사이즈와 네트워크 자체의 크기 때문이다. Krizhevsky의 돌파구로 800만 개의 매개변수를 가진 8개의 레이어로 구성된 대규모 네트워크를 ImageNet 데이터셋의 100만 개의 훈련 이미지로 supervised training한 사례가 있고 그 이후로, 더 크고 깊은 네트워크들이 훈련되었다.

 일반적으로 convolutional networks가 사용된 곳은 classification tasks이고 이는 이미지를 단일 클래스 label로 분류하는 문제이다. 그러나 많은 visual tasks, 특히 biomedical image processing은 이러한 output에 localization을 요구하였고 이는 우리가 아는 segmentation으로 각 pixel마다 class label을 assign하는 문제이다. 게다가 수천여장의 이미지가 주로 biomedical tasks에 존재한다.(확실히 적은 수치이다.) 따라서 Ciresan은 sliding-window setup을 통해 네트워크를 훈련하여 각 픽셀별 class label을 예측하고자 하였고 픽셀을 둘러싼 영역(이미지의 작은 부분인 패치)를 입력으로 삼았다. 먼저 이러한 네트워크는 localize가 가능했고 다음, patch를 입력으로 받기 때문에 training data의 개수는 images 전체를 입력받을 때보다 많았다. 그 결과 이 네트워크는 ISBI 2012 EM segmentation challenge 에서 큰 차이로 우승하였다.

 확실이 Ciresan의 전략은 두 가지 단점이 존재한다. 먼저, 네트워크가 각 패치마다 개별로 진행되어야 하기 때문에 매우 느렸고 patches 간의 overlapping으로 매우 많은 redundancy가 존재했다. 다음으로, localization accuracy와 use of context사이에 trade-off가 존재했다. 큰 패치는 많은 max-pooling layers를 요구하여 localization accuracy를 낮추었고, 반면 작은 패치는 네트워크가 작은 context만 보게 하였다. 더 최근 접근방법에는 classifier output을 multiple layers에서 설명하는 방법이 있어 good localization과 use of context가 동시에 가능하도록 한다.

 이 논문에서 우리는 더 세련된 구조인 fully convolutional network를 만들었다. 우리는 이 구조를 수정하고 확장하여 매우 작은 training images에서 precise segmentation을 수행하게 하였다. 

 FCN의 메인 아이디어(저번 포스팅에 올렸던 논문)는 일반적인 contracting network를 pooling operators를 upsampling operators로 대체한 succesive layers로 보충하는 것이다. 따라서 이 층은 output의 해상도를 중가시키니다. Localize를 위해서 contracting path의 high resolution feautres가 upsampled output과 결합한다. 이 연속적인 convolution layer은 정보의 output들을 ensemble 하여 학습한다.

 우리의 구조에서 중요한 수정은 upsampling part에서도 큰 숫자의 feature channels를 가졌다는 것이다. 이는 network가 higher resolution layers로 context information을 전달하도록 한다. 그 결과 expansive path는 거의 contracting path와 symmetric하여 u-shaped architecture을 구성하게 된다. 이 네트워크는 fully connected layers를 갖지 않고 각 합성곱의 유용한 부분만 사용한다. 즉, segmentation map은 입력 이미지에서 전체 context가 사용 가능한 pixels만 포함되는데 overlap-tile strategy를 추가로 사용하여 임의의 큰 이미지에서 매끄러운 segmentation이 가능하게 한다. 이미지의 경계에 해당하는 pixels를 예측하기 위해 missing context를 input image에 mirroring을 통해 extrapolate한다. 이 tiling strategy는 네트워크에 큰 이미지를 적용하는데 중요한데 왜나하면 이렇게 하지 않는 경우 GPU memory에 의해 제한될 수 있기 때문이다.

우리의 tasks는 매우 작은 training data가 이용가능하기 때문에 우리는 강력한 data augmentation인 elastic deformation을 training images에 수행한다. 이것은 network가 이러한 deformations에 대해 invariance를 갖게 만든다. 이는 특히 biomedical segmentation에서 아주 중요한데 왜냐하면 tissue에는 이러한 변형들이 자주 일어나고 실제의 변형들을 효과적으로 재현할 수 있기 때문이다. Unsupervised feature learning의 범위에서 learning invariance에 대한 data augmentation의 가치는 Dosovitsky에 의해 알려져있다.

 많은 cell segmentation에서 또다른 어려움은 same class의 접촉하는 objects를 분리하는 것이다. 마지막에 우리는 weigted loss를 제안하여 touching cells의 사이를 background labels로 여겨 분리하고 이 부분에 높은 가중치를 부여하는 loss function을 만들 것이다.

 결과적으로 생성된 network는 다양한 biomedical segmentation problems에 적용가능하다. 이 논문에서 우리는 EM stacks(an ongoing competition started at ISBI 2012)에서 segmentation of neuronal structures의 결과를 보여줄 것이고 우리는 이 대회에서 Ciresan의 결과를 뛰어넘었다. 뿐만 아니라, ISBI cell tracking challenge 2015의 light microscoy images cell segmentation에서의 결과를 보여줄 것이다. 우리는 2D trasmitted light datasets에서 큰 차이로 우승하였다.

< comment >

 저자들은 FCN의 구조를 확장하여 더 정확한 segementation이 가능한 구조를 만들었다. Expanding path(upsampling path)에 연속적인 layers를 보충하였고 많은 수의 채널을 갖게 설계하였다. 그 결과 두 경로가 대칭인 u-shape의 구조를 갖게 되었다. 또한 padding 없이 convolution을 수행하는 것이 특징인데 그럼 layer를 통과할 수록 크기가 줄어들어 이를 보충하기 위해 mirroring extraplation을 사용하였다. 뿐만 아니라 elastic deformation을 통한 data augmentation을 통해 작은 수의 이미지로도 충분한 성능을 내도록 하였고 instance segmentation을 수행하기 위해 touching cells 사이를 background처럼 인식하고 가중치를 부여하였다.

2. Network Architecture

< 내용 >

네트워크의 구조는 우와 같이 묘사되며 왼쪽의 contracting path와 오른쪽의 expanding path로 이루어진다. Contracting path는 일반적인 convolutional network의 구조를 따라한다. 이는 반복되는 두개의 3*3 convolutions(unpadded convolutions)로 이루어져있고 각각은 ReLU를 이어받는다. 그리고 2*2 max pooling operation with stride 2가 convolution layers 사이에 존재해 downsampling한다. 한번의 downsampling이 일어나면 feature channels는 두배가 된다. Expansive path의 모든 step에는 feature map의 채널 수를 절반으로 줄이는 2*2 합성곱 을 통해 upsampling하고 대응되는 크기로 잘라낸 contractin path의 결과와 연결된 후 두번의 3*3 합성곱(각각은 ReLU를 사용)으로 구성된다. . Cropping이 필수인데 every convolution에서 border pixels를 잃기 때문이다. 마지막 레이어의 1*1 convolution은 64개의 component feature vector을 요구되는 class의 숫자에 맞게 mapping하는데 쓰여 총 network는 23개의 convolution layers를 갖는다.

 Segmenatation map의 output이 매끄럽기 위해선 2*2 max-pooling operations에 들어가는 input tile size가 짝수여야 한다.

< comment >

구조는 contracting path와 expanding path로 이루어져 있고 segmentation이 매끄럽게 수행되기 위해선 2*2 max-pooling operations에 들어가는 tile의 사이즈가 짝수여야한다.

3. Training

< 내용 >

 Input image와 대응되는 segmentation maps는 Caffe에 구현된 stochastic gradient descent를 통해 훈련된다. Unpadded convolution 때문에 output image는 input image보다 작다.(by a constant border width) GPU memory의 overhead를 최소화하고 gpu를 최대로 사용하기 위해서 우리는 large input tiles를 large batch size보다 선호한다. 따라서 batch size를 1로 하여 단일 이미지를 사용하였다. 우리는 high momentum인 0.99를 사용하여 이전에 보았던 training samples들의 대부분이 current optimization step의 update에 사용되도록 하였다.

 Energy function은 마지막 feature map의 pixel-wise soft-max와 cross entropy loss function을 결합한 함수를 사용하였다. soft-max는 $p_k(\mathbf{x})=\textrm{exp}(a_k(\mathbf{x}))/(\sum_{k'=1}^{K}\textrm{exp}(a_k'(\mathbf{x})))$로 정의되고

$\textrm{exp}(a_k'(\mathbf{x}))$ 는 x( $\textbf{x}\in\Omega\space\text{with}\space\Omega\subset\mathbb{Z}^2$ )의 feature channel k의 activation을 의미한다. K는 classes의 number를 의미하고 $p_k(\mathbf{x})$는 approximated maximum function이다.

*approximated maximum function

일반적으로 cross-entropy loss에 log안에 들어가는 값은 실제 분포를 추정한 모델의 확률로 U-net의 마지막 layer의 출력값이다. 그러나 특정 layer의 값을 단순히 대입하는 것은 미분이 불가능하기 때문에 미분가능한 값으로 만들기 위해 approximation funtion을 사용한다.

즉 이 값이 1에 가깝다는 것은 대응되는 k에 대해 maximum activation을 갖는 것이고 다른 k에 대해서는 이 값이 0에 가깝다. Cross entropy는 $-\sum_{i=1}^np(x_i)log(q(x_i))$인데 class segmentation인 $p(x_i)$가 실제 레이블에서만 1이므로 최대화하려는 energy funtion은 다음과 같이 정의된다.

$$E=\sum_{\mathbf{x}\in\Omega}w(\mathbf{x})log(p_{l(x)}(\mathbf{x})) $$

여기서 l은 each pixel의 true label을 의미하고 w는 weight map으로 몇몇의 pixels에 더 중요하게 생각하기 위해 도입한 것이다.

 먼저 우리는 wegith map을 certatin class의 different frequency of pixels를 반영하여 보상하기 위해 pre-compute한다. 이후에 가중치를 update하여 touching cells 사이에 있는 small separation borders도 학습할 수 있게 한다.

가중치 update는 morphological operations(형태학적 작용)을 통해 계산되는데 식은 다음과 같다.

$$w(\mathbf{x})=w_c(\mathbf{x})+w_0\cdot\textrm{exp}(-\frac{(d_1(\mathbf{x})+d_2(\mathbf{x}))^2}{2\sigma^2})$$

$w_c$는 class frequencies를 balance한 weight map이고 $d_1$은 가장 가까운 셀의 경계 까지의 거리, $d_2$는 두번째 가까운 셀의 경계까지의 거리이다. 우리의 실험에는 $w_0=10$, $\sigma\approx5$ pixels이다.

 Deep networks에서 많은 convolution layers와 network를 통과하는 다양한 경로가 존재하면 weights의 초기 initialization은 매우 중요하다. 그렇지 않으면 네트워크의 일부가 과도하게 활성화되어 다른 부분은 전혀 기여하지 않을 수 있다. 이상적으로는 네트워크의 각 피처 맵이 단위 분산을 갖도록 초기 가중치를 정해야 한다. 교대로 발생하는 convolution 과 ReLU layers가 있는 우리의 구조에서는 이 목표를 달성하기 위해 표준 편차가 $\sqrt{2/N}$인 가우시안 분포에서 초기 가중치를 추출하였다. 여기서 N은 한 뉴런의 입력 노드 수를 의미한다. 예를 들어 이전 층에 64개의 채널이 있는 3*3 합성곱의 경우 N은 9*64=576이다.

3.1 Data Augmentation

Data augmentation은 매우 적은 training samples가 이용가능할 때 network에 invariance와 robustness properties를 가르치는데 필수적이다. Microscopial images의 경우 우리는 주로 여러 변형에 대한 robustness 뿐만아니라 shift와 rotation invariance, gray value varations에 대한 invariance 까지 필요하다. 특히 random elastic deformations를 training sample에 적용하는 것이 매우 적은 annotated images에서 segmentation을 수행하는 network를 훈련시킬 때 주요해보인다. 우리는 3*3 격자에서 랜덤한 변위 벡터를 사용하는 smooth deformations를 생성하였다. 변위는 표준 편차가 10 픽셀인 가우시안 분포에서 샘플링하였다. 각 픽셀의 변위는 bicubic interpolations에 의해 계산된다. 수축 경로 끝에 있는 Drop-out layers는 암묵적인 data augmentation을 추가적으로 수행한다.=

< comment >

U-Net은 biomedical image의 사이즈가 크다는 특성 때문에 patchwise training을 사용한다. 이 과정에서 큰 input tiles를 선호해 batchsize는 최소화하여 1을 사용하였다. 또한 optimize할 때 momentum을 0.99인 큰 값을 사용하여 이전 이미지가 현재에 대부분 영향을 주도록 설계하였다.

 Loss funtion은 pixel-wise softmax function과 cross-entropy loss를 결합하여 설계하였고 weight를 도입하여 class간의 frequency, touching cells 사이에 위치했는가를 반영하였다. 그리고 중요한 초기 가중치 설계를 입력 노드를 고려한 가우시안 분포에서 추출하였다.

4. Experiments

< 내용 >

< comment >

U-Net은 다양한 bio-medical image segmentation에서 좋은 성능을 보인다.

5. Conclusion

< 내용 >

 U-net 구조는 다양한 biomedical segmentation applications에서 좋은 성능을 달성하였다. Elastic deformations를 사용하는 data augmentation에 힘입어 매우 작은 annotated imges만 필요하고 타당한 training time을 소요한다. Caffe-based implementation과 trained networks를 제공한다. 우리는 u-net architecture이 다른 더 많은 tasks에서 쉽게 적용될 것을 장담한다.

< comment >

U-net은다양한 biomedical segmentation application에서 좋은 성능을 보이고 사용한 주요 techniques는 u-shaped architecture(with layers and channels), overlap-tile strategy & mirroring extrapolation, data augementation(by. elastic deformation)이다.